- #1
epsilon
- 29
- 1
The direction of the torques in the following working will be found using: [itex]\vec{\tau} = \vec{r} \times \vec{F}[/itex].
When viewed from above, the counterclockwise rotation of the blades produces a torque out of the page:
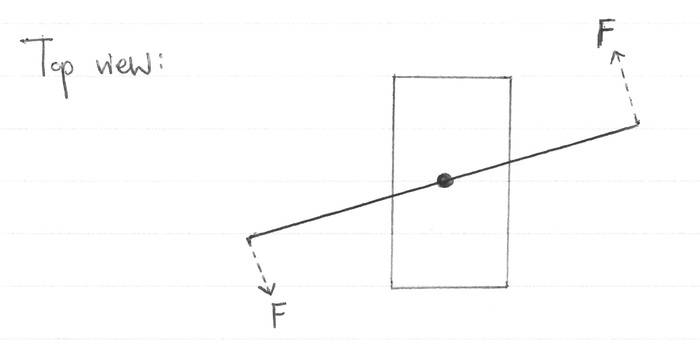
As the angular momentum (right-hand corkscrew rule) is also out of the page, the body will begin to rotate clockwise to conserve the angular momentum.
The direction of the torque associated with this rotation of the body will be into the page:
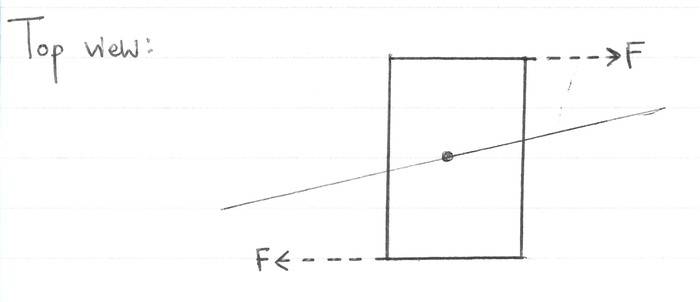
Hence we have a torque into the page, and a torque out of the page. Q1) If these torques are in opposite directions, why are these not sufficient to cancel out the rotation and keep the body steady?
The tail rotor is added to do this job (as I have been told infinitely-many times). By considering a side view of the helicopter, and a tail rotor with a clockwise rotation, it will produce a torque that is out of the page in this view.
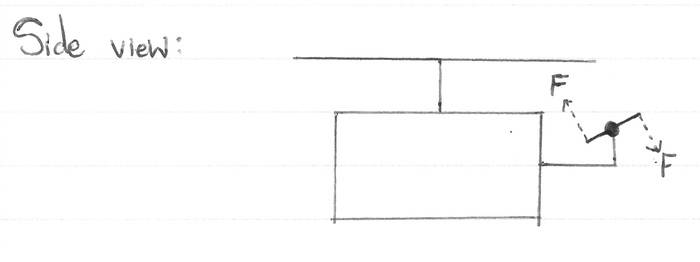
If the helicopter is re-considered from a birds-eye view, the tail rotor has produced a sideways torque. Hence the torque on the body due to the main rotor, and the torque of the tail rotor are perpendicular - how can they cancel one another out?
I know that I have a misunderstanding somewhere, hence why I have written this thread. I find rotations by far the most difficult part of mechanics to grasp and am really struggling with it, plus I need to be able to extent this knowledge to the behaviour of gyroscopes too (not looking good).
If you are able to clear the above problem up for me, and give me any advice on how to best solve rotations problems I would be very grateful.
When viewed from above, the counterclockwise rotation of the blades produces a torque out of the page:
As the angular momentum (right-hand corkscrew rule) is also out of the page, the body will begin to rotate clockwise to conserve the angular momentum.
The direction of the torque associated with this rotation of the body will be into the page:
Hence we have a torque into the page, and a torque out of the page. Q1) If these torques are in opposite directions, why are these not sufficient to cancel out the rotation and keep the body steady?
The tail rotor is added to do this job (as I have been told infinitely-many times). By considering a side view of the helicopter, and a tail rotor with a clockwise rotation, it will produce a torque that is out of the page in this view.
If the helicopter is re-considered from a birds-eye view, the tail rotor has produced a sideways torque. Hence the torque on the body due to the main rotor, and the torque of the tail rotor are perpendicular - how can they cancel one another out?
I know that I have a misunderstanding somewhere, hence why I have written this thread. I find rotations by far the most difficult part of mechanics to grasp and am really struggling with it, plus I need to be able to extent this knowledge to the behaviour of gyroscopes too (not looking good).
If you are able to clear the above problem up for me, and give me any advice on how to best solve rotations problems I would be very grateful.