Help Calculate Work Done in Adiabatic Process & Fill Table

[Callmelucky]

Homework Statement

How to calculate work in cycle process that consists of isothermal, isobaric and adiabatic processes.

Relevant Equations

deltaU=Q-W, Q=W, Q=-W,

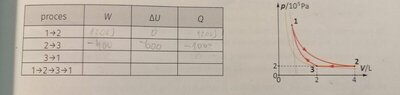
(picture of diagram below)So the task goes like this: gas is ideal. Process 3->1 s adiabatic and in process 1->2 work done is 1200J. Fill the table.
I don't know how to calculate work done in an adiabatic process because p2 and V2 are not given and I don't know gama(Cp/Cv).
I know that deltaU of the entire process is 0. So if I am thinking correctly work done should be 800J because work done from 2->3 is -400J(first two processes are correct) and that is energy gained back, so to reach 1200J of work we need 800J more, but it's not. Apparently work done in 3->1 is -600J, deltaU= 600J and Q=0. And total work done is 200J, deltaU=0, and Q= 200J.

Please help me.

 

[Callmelucky]

P.S. the line between 0 and 2 is my handiwork. It's not given by authors so I don't think I should use it.

 

[TSny]

work done from 2->3 is -400J

OK. But you should show or explain how you got this.

How did you get $\Delta U = -600$ J and $Q = -1000$ J for process 2 -> 3?

 

[Callmelucky]

OK. But you should show or explain how you got this.

How did you get $\Delta U = -600$ J and $Q = -1000$ J for process 2 -> 3?

Well process is isobaric so W=pdeltaV, and deltaU = U2 - U1. U2= 3/2p2V2, U1=3/2p1V1. Q=deltaU+W

 

[TSny]

deltaU = U2 - U1. U2= 3/2p2V2, U1=3/2p1V1.

The factor of 3/2 indicates that you are working with a monatomic ideal gas. But in your summary of the statement of the problem, there is no indication that the gas is monatomic. It is always best to type in the statement of the question word for word as it was given to you.

 

[Callmelucky]

The factor of 3/2 indicates that you are working with a monatomic ideal gas. But in your summary of the statement of the problem, there is no indication that the gas is monatomic. It is always best to type in the statement of the question word for word as it was given to you.

well, I have no idea then. Any suggestions? Just point me in the right direction. All infos I have are in description of the problem.

 

[Callmelucky]

The factor of 3/2 indicates that you are working with a monatomic ideal gas. But in your summary of the statement of the problem, there is no indication that the gas is monatomic. It is always best to type in the statement of the question word for word as it was given to you.

But it doesn't even matter because what’s the point of saying that ideal gas is made of monoatomic/polyatomic molecules if they still have zero volume?

 

[TSny]

If the gas is given to be monatomic, then I agree with your results for processes 1 -> 2 and 2 -> 3.

So if I am thinking correctly work done should be 800J because work done from 2->3 is -400J(first two processes are correct) and that is energy gained back, so to reach 1200J of work we need 800J more, but it's not.

Here, it appears to me that you believe that the total work done for the three individual processes should add to zero. That would make the total work done for the cycle equal to zero. But, that isn't true. (The work done for the cycle equals the area enclosed by the cycle on the PV diagram.) But maybe I'm misinterpreting what you are saying. Anyway, I'm not following your reasoning here.

 

[Callmelucky]

If the gas is given to be monatomic, then I agree with your results for processes 1 -> 2 and 2 -> 3.
Here, it appears to me that you believe that the total work done for the three individual processes should add to zero. That would make the total work done for the cycle equal to zero. But, that isn't true. (The work done for the cycle equals the area enclosed by the cycle on the PV diagram.)

No, deltaU=0, work done by the cycle should equal heat received + energy from work in process 2->3. But I can't calculate deltaU for adiabatic process or work done by adiabatic process. That + work done from 2->3 would equal the heat recieved by the system to do work of 1200J. Right? Or I got something wrong?

 

[kuruman]

You need to be systematic and fill in the Table with the appropriate entries. Start by finding the temperatures at the three points. You $V_3$ and $p_3$, so you can find $T_3$. Knowing that and the adiabatic condition, you can find $T_1$ and hence $T_2$. Once you have the temperatures, you can fill in the $\Delta U$ entries. Then come the works and heats at each leg of the cycle. Unless the problem states otherwise, I would assume that the gas is monatomic so that $C_V=\frac{3}{2}R$.

When the Table is completely filled, you can check your work for consistency. The sum of the $\Delta U$ entries must be zero and the the sum of all the $Q$ entries must be the negative of the sum of all the $W$ entries. Furthermore, the $\Delta U$ in each row must be equal to $Q-W$ in that row.

 

[TSny]

No, deltaU=0, work done by the cycle should equal heat received + energy from work in process 2->3.

I'm not following. For the cycle, $\Delta U = 0$. So the work done by the gas for the cycle equals the heat gained for the cycle. So, I don't understand why you say that the "work done by the cycle should equal the heat received + energy from work in process 2->3".

But I can't calculate deltaU for adiabatic process or work done by adiabatic process. That + work done from 2->3 would equal the heat recieved by the system to do work of 1200J. Right? Or I got something wrong?

I'm sorry, but this is not making sense to me.

Suppose you let $x$ represent the unknown amount of work done in the adiabatic process 3 -> 1. Can you fill in the table for 3 -> 1 in terms of $x$?

 

[Callmelucky]

ohh yess. I completely forgot about that. Thank you @kuruman

 

[TSny]

But it doesn't even matter because what’s the point of saying that ideal gas is made of monoatomic/polyatomic molecules if they still have zero volume?

I don't know what you have covered so far in your course. For classical ideal gases, a polyatomic gas at pressure P and volume V has more internal energy U than a monatomic gas at the same pressure and volume. Monatomic molecules have only translational kinetic energy. Polyatomic molecules can store energy in rotational and vibrational motion as well as translational motion. The formula U = (3/2)PV is valid for a monatomic ideal gas but not for a polyatomic gas.

 

[Chestermiller]

Please provide the exact word-for-word statement of this problem. You seem to have omitted some important information.

 

[Callmelucky]

Please provide the exact word-for-word statement of this problem. You seem to have omitted some important information.

I did. This is a literal description of the problem; gas is ideal. Process 3->1 s adiabatic and in process 1->2 work done is 1200J. Fill the table.

 

[Callmelucky]

I don't know what you have covered so far in your course. For classical ideal gases, a polyatomic gas at pressure P and volume V has more internal energy U than a monatomic gas at the same pressure and volume. Monatomic molecules have only translational kinetic energy. Polyatomic molecules can store energy in rotational and vibrational motion as well as translational motion. The formula U = (3/2)PV is valid for a monatomic ideal gas but not for a polyatomic gas.

There is literally no word about such a thing in my textbook(but I am not saying you are wrong). But I have watched some videos of Micael Von Biezen on YT, and he was mentioning Cv and Cp, heat capacities for isochoric and isobaric change, I don't know if that is what you think, but even if it is there is nothing about that in my textbook. And the reason I have said that it doesn't matter if it's monoatomic or diatomic is that in my textbook it's stated that molecules of gas do not occupy volume while gas itself does. And I have found same statement on quora by some guy who has Ph.D. in chemistry. Here is the link https://www.quora.com/Is-it-necessary-that-ideal-gases-are-monatomic

Edit: I have just finished the cycle process in thermodynamics(that is what I have covered this year so far).

 

[kuruman]

You can calculate all the Table entries individually and use the first law to check your work. As I indicated earlier, you start by finding the temperatures. My opinion is that in intro level thermo problems all gases are ideal and monatomic unless there is explicit information to the contrary. This means that $C_V=\frac{3}{2}R$ and $C_p=\frac{5}{2}R$. Here is what I recommend.

1. Start with $T_3$ because you know $p_3$ and $V_3$. Then finding $T_2$ is easy and finding $T_1$ is trivial. This will pave the way for finding the three $\Delta U$ entries assuming that the gas is monatomic.
2. Find the work done by the gas during each process. You will need to derive expressions for the adiabatic and isothermal legs if you don't remember them.
3. Find the heat entering the gas for each process. You know that $Q=0$ for the adiabatic and $Q=W$ for the isothermal. What is the relevant equation for the heat entering the gas at constant pressure?

When you complete the above 3 steps, you're done.

 

[Callmelucky]

You can calculate all the Table entries individually and use the first law to check your work. As I indicated earlier, you start by finding the temperatures. My opinion is that in intro level thermo problems all gases are ideal and monatomic unless there is explicit information to the contrary. This means that $C_V=\fac{3}{2}R$ and $C_p=\fac{5}{2}R$. Here is what I recommend.

1. Start with $T_3$ because you know $p_3$ and $V_3$. Then finding $T_2$ is easy and finding $T_1$ is trivial. This will pave the way for finding the three $\Delta U$ entries assuming that the gas is monatomic.
2. Find the work done by the gas during each process. You will need to derive expressions for the adiabatic and isothermal legs if you don't remember them.
3. Find the heat entering the gas for each process. You know that $Q=0$ for the adiabatic and $Q=W$ for the isothermal. What is the relevant equation for the heat entering the gas at constant pressure?

When you complete the above 3 steps, you're done.

I have. Thank you. I understand now. You didn't have to write all over again. I understood everything from the first reply. I answered others because I wanted to hear what they have to say. Your comment helped me a lot.

 

[Callmelucky]

You can calculate all the Table entries individually and use the first law to check your work. As I indicated earlier, you start by finding the temperatures. My opinion is that in intro level thermo problems all gases are ideal and monatomic unless there is explicit information to the contrary. This means that $C_V=\fac{3}{2}R$ and $C_p=\fac{5}{2}R$. Here is what I recommend.

1. Start with $T_3$ because you know $p_3$ and $V_3$. Then finding $T_2$ is easy and finding $T_1$ is trivial. This will pave the way for finding the three $\Delta U$ entries assuming that the gas is monatomic.
2. Find the work done by the gas during each process. You will need to derive expressions for the adiabatic and isothermal legs if you don't remember them.
3. Find the heat entering the gas for each process. You know that $Q=0$ for the adiabatic and $Q=W$ for the isothermal. What is the relevant equation for the heat entering the gas at constant pressure?

When you complete the above 3 steps, you're done.

What really bothers me is that there really is nothing about Cv and Cp in my textbook. Most of the formulas I have are from Michael Van Biezen's channel on YT (https://www.youtube.com/@MichelvanBiezen), this guy is literally saving my life. Half of the things(if not more) I need are not in my textbook.

 

[kuruman]

What really bothers me is that there really is nothing about Cv and Cp in my textbook. Most of the formulas I have are from Michael Van Biezen's channel on YT (https://www.youtube.com/@MichelvanBiezen), this guy is literally saving my life. Half of the things(if not more) I need are not in my textbook.

That bothers me too. However, for this particular problem, you don't need $C_V$ and $C_p$ if you use the first law after you find all the $\Delta U$ entries. You can determine the $Q$ and $W$ entries by demanding that the first law be satisfied to find what's missing. However, I don't think that this is instructive. That is why I suggested that you find the entries independently and verify that the fist law is satisfied during each step.