{ help } Calculating the B-field at the center of a solenoid

[Special One]

Homework Statement

Explain how did we get the formula used in the question answer.

Relevant Equations

Magnetic field

Problem 52:
A solenoid is 40 cm long, has a diameter of 3.0 cm, and is wound with 500 turns. If the current through the windings is 4.0 A, what is the magnetic field at a point on the axis of the solenoid that is (a) at the center of the solenoid, (b) 10.0 cm from one end of the solenoid, and (c) 5.0 cm from one end of the solenoid? (d) Compare these answers with the infinite-solenoid case.

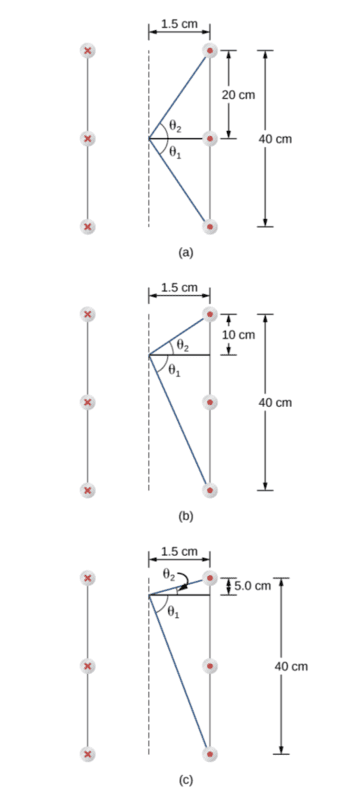
I didn't get the second half of the formula, which is ( sinΘ2-sinΘ1 ) ?
And why when we substitute we consider the Θ1 as negative??

 

[kuruman]

Is the posted work under Problem 52 your attempt at a solution? If yes, then you should know where the $(\sin\theta_2-\sin\theta_1)$ term came from; it has to do with the fact that the solenoid is finite. If that's someone else's solution, please post your attempt and we'll take it from there. Once you have correctly derived (with perhaps some help) your own equation, then you will know why $\theta_1$ is taken negative.