- #1
donniemsb_12
- 25
- 0
this problem was discussed by our professor . but I am a lil bit confused on it ! thanks ! help !
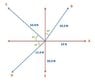
FIVE COPLANAR FORCES ACT ON AN OBJECT AND THEIR RESULTANT !
our prof use this formula !
Bx=Bsin(degree)
By=Bcos(degree)
ANSER:
VECTORS X-COMPONENTS Y-COMPONENTS
A 19.0 0
B 7.5 12.99
C -11.31 11.31
D -9.53 -5.5
E 0 -22.0
Σx=5.66 Σy=-3.2
MY QUESTION IS : HOW TO KNOW IF WHAT PARTICULAR OPERATION TO BE USE ON EACH OF THE COMPONENTS ? WHEN WILL I USE THE SIN FUNCTION AND COSINE FUNCTION IN GETTING THE COMPONENTS? THANKS !
FIVE COPLANAR FORCES ACT ON AN OBJECT AND THEIR RESULTANT !
our prof use this formula !
Bx=Bsin(degree)
By=Bcos(degree)
ANSER:
VECTORS X-COMPONENTS Y-COMPONENTS
A 19.0 0
B 7.5 12.99
C -11.31 11.31
D -9.53 -5.5
E 0 -22.0
Σx=5.66 Σy=-3.2
MY QUESTION IS : HOW TO KNOW IF WHAT PARTICULAR OPERATION TO BE USE ON EACH OF THE COMPONENTS ? WHEN WILL I USE THE SIN FUNCTION AND COSINE FUNCTION IN GETTING THE COMPONENTS? THANKS !