- #1
ryley
- 20
- 2
- Homework Statement
- I'm having difficulty seeing how to take math and apply it to the situation. Or recognizing when I can use a technique.
- Relevant Equations
- Fnetx=0
Fnety=0
Fnetz=0
Hello all, thanks for reading my post! I'm posting as I need help with my problem solving and thinking approach. For the most part I can figure out how to set up the problem and what I need to find, but my problem lies in textbook questions that rely more on seeing a more math based approach to solving rather than thinking about the concepts. What I mean is, the concepts are easy to see but minimal information is given leaving multiple variables and so methods like substitution are needed as well as other algebraic techniques. I'll post a question that this applies to and show my thinking process as well as a diagram. If anyone is able to help me identify what exactly it is I'm doing wrong so as to help me determine a solution to a problem it would be greatly appreciated.
Question
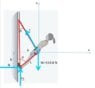
A climber with a weight of 533.8 N is held by a belay rope connected to her climbing harness and belay device; the force of the rope on her has a line of action through her center of mass. The indicated angles are 30 degrees(top) and 40 degrees(bottom). If her feet are on the verge of slipping on the vertical wall, what is the coefficient of static friction between her climbing shoes and the wall?
First thoughts
- I will need to sum the forces in x and y directions as well as torques.
- doing this yields a few unknowns and I can't seem to see a way to solve for one and sub it in or equate any of them.
- I think It will be best to use her foot contacting the wall as the origin to eliminate the Fs and FN from the torque equations, but that still leaves me with tension as an unknown.
- The force net equations also have unknowns that I can't see a way to solve for.
This Is where I get stuck and can't see a way to solve for what I need as its not about applying concepts anymore instead it is more math. The solution shows to use some substitution as well as equating two equations, this isn't the hard part to solve as I can do the algebra but its seeing that, that is what I'm suppose to do that I'm having trouble realizing.
I'll attach a picture of the diagram as well as the solution.
Thanks for any help!
Question
A climber with a weight of 533.8 N is held by a belay rope connected to her climbing harness and belay device; the force of the rope on her has a line of action through her center of mass. The indicated angles are 30 degrees(top) and 40 degrees(bottom). If her feet are on the verge of slipping on the vertical wall, what is the coefficient of static friction between her climbing shoes and the wall?
First thoughts
- I will need to sum the forces in x and y directions as well as torques.
- doing this yields a few unknowns and I can't seem to see a way to solve for one and sub it in or equate any of them.
- I think It will be best to use her foot contacting the wall as the origin to eliminate the Fs and FN from the torque equations, but that still leaves me with tension as an unknown.
- The force net equations also have unknowns that I can't see a way to solve for.
This Is where I get stuck and can't see a way to solve for what I need as its not about applying concepts anymore instead it is more math. The solution shows to use some substitution as well as equating two equations, this isn't the hard part to solve as I can do the algebra but its seeing that, that is what I'm suppose to do that I'm having trouble realizing.
I'll attach a picture of the diagram as well as the solution.
Thanks for any help!