- #1
Saladsamurai
- 3,020
- 7
Help! Force of a Spring for "Small" displacements
Okay, here is the diagram,
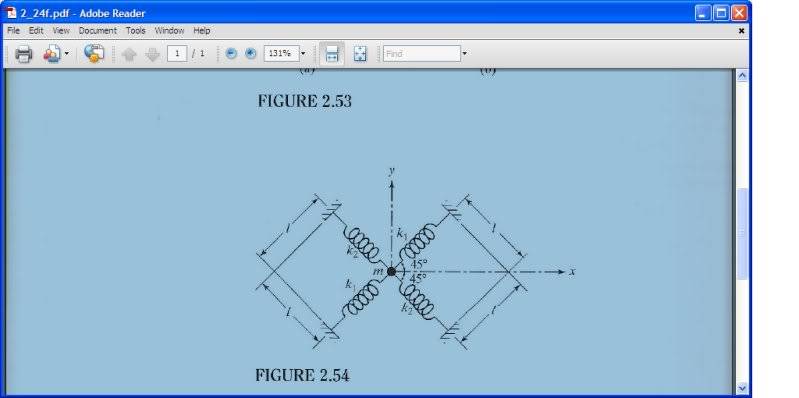
For "small horizontal displacements" of the mass:
For the force exerted by each spring (TOTAL, not resolved) they are using:
Fsp=kxcos(45) and then resolving it onto the x-axis they use
Fsp x=kxcos25*cos45
I do not understanding this at all.
Why is the unresolved force using cos*45 ?
I am thinking it has to do with the fact that we are assuming that we are making
only "small horizontal displacements" of the mass.
Homework Statement
Okay, here is the diagram,
For "small horizontal displacements" of the mass:
For the force exerted by each spring (TOTAL, not resolved) they are using:
Fsp=kxcos(45) and then resolving it onto the x-axis they use
Fsp x=kxcos25*cos45
I do not understanding this at all.
Why is the unresolved force using cos*45 ?
I am thinking it has to do with the fact that we are assuming that we are making
only "small horizontal displacements" of the mass.