MichaelTam
- 93
- 6
- Homework Statement
- Exercise
- Relevant Equations
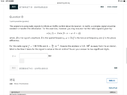
- ##v = f \lambda , s({x,t}) = A sin({k x - \omega t + \phi}) ##, other statements are provided in the picture.
I know so ## y = A sin({2*10^6 ({\pi / 3 -\pi t }) + \phi }) ##
There still some unknown I cannot find, can anyone give me some hint please?
There still some unknown I cannot find, can anyone give me some hint please?
Attachments
Last edited: