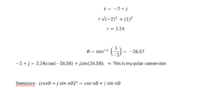Eng studies
- 13
- 0
- Homework Statement
- Convert to polar form and find z'8 using de moivre theorem, plot on argand diagram
- Relevant Equations
- Demoivre - (cos0+jsin0)'n = cosn0 +jsinno
Hi all any help on this would be great I cant seem to progress with the theorem,
z= -2 + j > R sqrt (-2)'2 + (-1)'2
r = 2.24
0= Arctan(-1) = 26.57 Polar form = 2.24(cos(26.58)+jsin(26.58)
-2
Demoivre - (cos0+jsin0)'n = cosn0 +jsinno
Could some one work a similar example to assist me through applying this ?
Thanks
z= -2 + j > R sqrt (-2)'2 + (-1)'2
r = 2.24
0= Arctan(-1) = 26.57 Polar form = 2.24(cos(26.58)+jsin(26.58)
-2
Demoivre - (cos0+jsin0)'n = cosn0 +jsinno
Could some one work a similar example to assist me through applying this ?
Thanks