Help Solve for the normalization constant of this QM integral

[casparov]

Homework Statement

find A

Relevant Equations

psi = A exp [ - x^2 / (2+ix) ]

I'm given the wavefunction

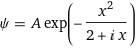
and I need to find the normalization constant A.

I believe that means to solve the integral

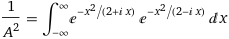
The question does give some standard results for the Gaussian function, also multiplied by x to some different powers in the integrand, but I can't seem to get it into that form.
Whatever I do, I get an x in the denominator of the exponent, and makes it impossible to solve for me.

 

[DrClaude]

I'm given the wavefunction

View attachment 326989

and I need to find the normalization constant A.

I believe that means to solve the integral

View attachment 326990

That is correct. However, this integral does not converge, so the given wave function is not normalizable (hence not a valid wave function).

 

[casparov]

That is correct. However, this integral does not converge, so the given wave function is not normalizable (hence not a valid wave function).

Sorry for the misplacement, it was a question on a final exam. Seems super odd to give this when the follow up questions implied it was normalizable. Thank you very much. Contacted my professor

 

[DrClaude]

Sorry for the misplacement, it was a question on a final exam. Seems super odd to give this when the follow up questions implied it was normalizable. Thank you very much. Contacted my professor

Could it be a typo?
$$
\psi = A \exp \left(- \frac{x^2}{2} + i x \right)
$$
would make more sense from a quantum mechanical point of view.