- #1
JenniferBlanco
- 47
- 0
I'm having a tough time solving this question. I'd appreciate it if someone can please help me out
I'd appreciate it if someone can please help me out
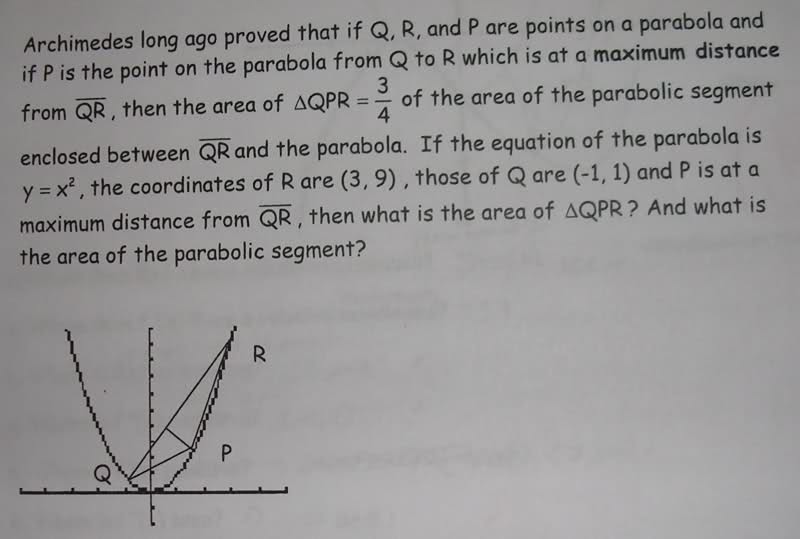
y=x^2
Triangle QPR =3/4 of the area of the parabolic segment enclosed between QR and the parabola
I don't know where to start :(
Homework Statement
Homework Equations
y=x^2
Triangle QPR =3/4 of the area of the parabolic segment enclosed between QR and the parabola
The Attempt at a Solution
I don't know where to start :(