gnits
- 137
- 46
- Homework Statement
- To find possible angle of two leaning rods
- Relevant Equations
- moments
Could I please ask for help with the following question:

The last part follows easily from the first part.
Answer from back of book for first part is:
2/(3u') <= tan(Ɵ) <= 2u
What I have done is the following:
Here's my diagram (I have separated the components to show the internal forces in the system. I have used t instead of Ɵ) :
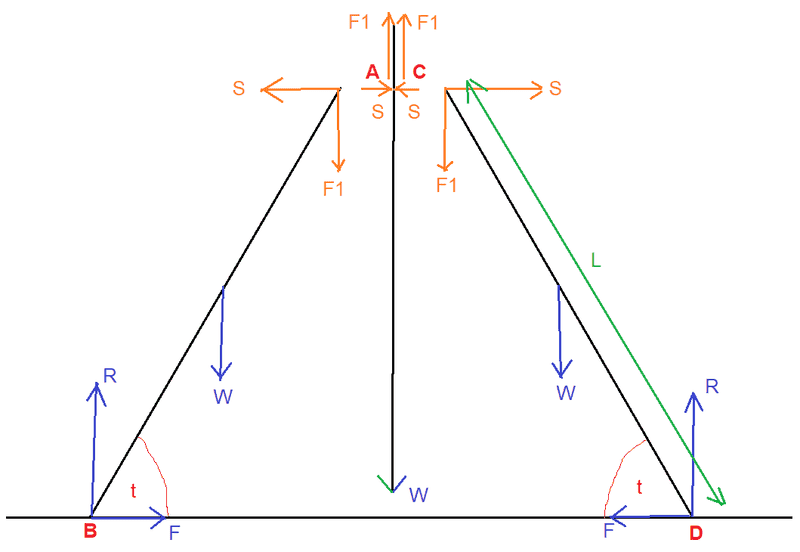
Orange forces are internal forces.
If I equate forces for the whole system vertically I get:
R = (3/2)W
If I equate forces vertically for the vertical rod only I get:
F1 = W/2
If I take clockwise moments about C for rod CD only I get:
F * L sin(t) + W * (L/2) cos(t) = R * L cos(t)
Substituting for R and rearranging gives: F = W / tan(t)
Now for no slipping at D we need F <= u' R so this gives:
W/tan(t) <= u' * (3/2)W
Which leads to tan(t) <= 2/(3u') which is the answer asked for but with the sign reversed.
1) How have I gotten the sign mixed up?
Taking clockwise moments about D for rod CD only I get:
S * L sin(t) = F1 * L cos(t) + W * (L/2) * cos*(t)
Substituting for F1and rearranging gives:
S = W/tan(t) and for no slipping at C we need S <= u * F1
So gives W/tan(t) <= u * W/2 which leads to tan(t) >= 2/u
Again wrong direction of sign and also wrong answer as we need tan(t) <= 2u
2) Where have a erred?
Thanks for any help.
The last part follows easily from the first part.
Answer from back of book for first part is:
2/(3u') <= tan(Ɵ) <= 2u
What I have done is the following:
Here's my diagram (I have separated the components to show the internal forces in the system. I have used t instead of Ɵ) :
Orange forces are internal forces.
If I equate forces for the whole system vertically I get:
R = (3/2)W
If I equate forces vertically for the vertical rod only I get:
F1 = W/2
If I take clockwise moments about C for rod CD only I get:
F * L sin(t) + W * (L/2) cos(t) = R * L cos(t)
Substituting for R and rearranging gives: F = W / tan(t)
Now for no slipping at D we need F <= u' R so this gives:
W/tan(t) <= u' * (3/2)W
Which leads to tan(t) <= 2/(3u') which is the answer asked for but with the sign reversed.
1) How have I gotten the sign mixed up?
Taking clockwise moments about D for rod CD only I get:
S * L sin(t) = F1 * L cos(t) + W * (L/2) * cos*(t)
Substituting for F1and rearranging gives:
S = W/tan(t) and for no slipping at C we need S <= u * F1
So gives W/tan(t) <= u * W/2 which leads to tan(t) >= 2/u
Again wrong direction of sign and also wrong answer as we need tan(t) <= 2u
2) Where have a erred?
Thanks for any help.