natalia
- 6
- 0
Hi,
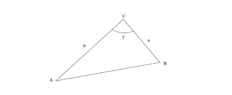
I have the following problem : Area of a triangle is given by S = 1/2 ab sin(γ) (See figure).
Discuss numeric conditioning of S. Any tips appreciated :D
View attachment 2493
I have the following problem : Area of a triangle is given by S = 1/2 ab sin(γ) (See figure).
Discuss numeric conditioning of S. Any tips appreciated :D
View attachment 2493