- #1
mdaugird
- 10
- 0
Please find attached a spreadsheet trying to plot an inductive/resistive circuit in the time domain and show instantaneous power and Volt Amperes.
Logic tells me power can not go negative, but I am not sure my power plot is correct.
Can someone please review the spreadsheet and chart to tell me if I am doing anything wrong?
I divided the VA and Power by 100 just to make the curves fit the graph. If my equations are correct i will address the formatting and second y-axis scale. How do I
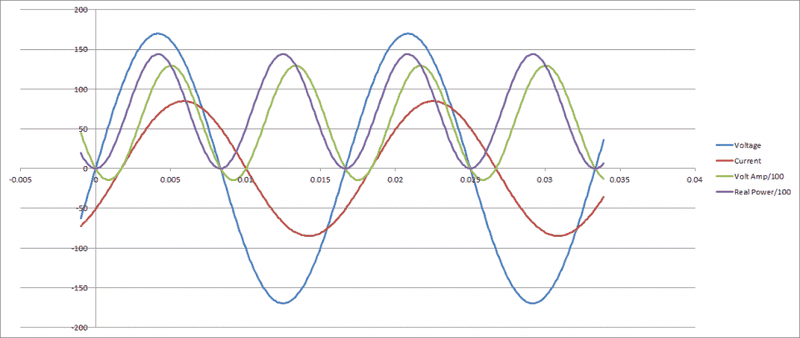 attach a spreadsheet?
attach a spreadsheet?
http://www.daugird.com\Book1.xlsx
Logic tells me power can not go negative, but I am not sure my power plot is correct.
Can someone please review the spreadsheet and chart to tell me if I am doing anything wrong?
I divided the VA and Power by 100 just to make the curves fit the graph. If my equations are correct i will address the formatting and second y-axis scale. How do I
http://www.daugird.com\Book1.xlsx
Last edited by a moderator: