Help to model transmission of forces through a medium

[Juanda]

TL;DR Summary

Simple models of springs do not consider the speed of sound of the medium to transmit the forces. I would like to be able to understand and model a situation like that.

Let's assume a system composed of 2 masses connected by a linear spring resting on a horizontal, frictionless table.

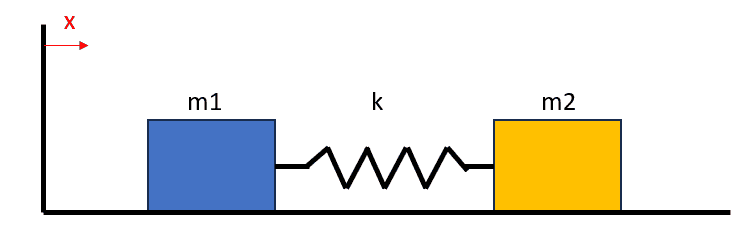
If I apply a force on $m_1$ its possition will change and INMEDIATELY produce a force on $m_2$ due to the spring connecting them. This is tipically an accepted approximation to reality but it is known that the force through the spring can only travel at the propagation speed of the medium. Since that speed is often very big and the mass of the spring is negligable, the instantenous approximation makes sense almost always. However, I would like to be able to model it more realistically even if it is not that practical. Or, at least, not practical in any case I can imagine now.

Springs are actually pretty complex geometries. As a simplification, let's say we have a connecting rod so its stiffness will be $k=\frac{EA}{L}$ where $E$ is the youg modulus, $A$ is the area of the cross section and $L$ is the undeformed length of the rod. Also, assume the rod has a linear density $\rho$ or assume its mass (whichever you find more convenient).

Secondly, the problem already feels hard enough by adding the inertia of the spring so to avoid having to deal with $m_1$ and $m_2$ let's just get rid of one of them. Then, imagine the force is applied at the end of the rod.

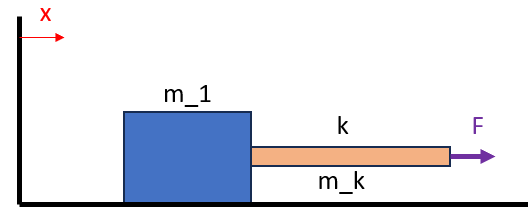
How would you model the dynamic behavior of such a problem to see how it evolves with time?

 

[Baluncore]

You will need to consider the blocks as acoustic transmission lines with acoustic impedance mismatches at the interfaces. There will be reflection and transmission coefficients at each interface. That will result in reflected waves travelling back down the lines to be reflected again, and again.

There is also an issue dealing with the modes of axial compressive waves. When those waves encounter a step change in diameter, there will be some other radial and shear mode excited.

You must define the spectrum of the initial excitation. That energy will be filtered by the length of the transmission line elements. You will need to identify how energy will be lost from the system, or if it will ring forever like a perfect bell.

A spring is a complex slow-wave structure, whereas the rod is a fast-wave structure, and so will be easier to model.

 

[Juanda]

You will need to consider the blocks as acoustic transmission lines with acoustic impedance mismatches at the interfaces. There will be reflection and transmission coefficients at each interface. That will result in reflected waves travelling back down the lines to be reflected again, and again.

There is also an issue dealing with the modes of axial compressive waves. When those waves encounter a step change in diameter, there will be some other radial and shear mode excited.

You must define the spectrum of the initial excitation. That energy will be filtered by the length of the transmission line elements. You will need to identify how energy will be lost from the system, or if it will ring forever like a perfect bell.

A spring is a complex slow-wave structure, whereas the rod is a fast-wave structure, and so will be easier to model.

This answer shows me I clearly lack the tools to derive a model for a system like this. Not even doing all the simplifications in the world (no dissipation of energy, constant rod diameter, uniform mass distribution in the rod, linear elastic behavior of the rod, mass being pushed is a rigid body, etc.) I would be able to put it all in equations.

The closest I could get is to change the rod with multiple masses all connected by massless springs but I wanted to know if there was a simple approach to solve this I was not aware of. I thought it could be interesting to model it and reduce Young's Modulus enough so that the effect of wave propagation can be seen.

 

[Baluncore]

This answer shows me I clearly lack the tools to derive a model for a system like this.

I might translate it into an electrical analog, then model it with SPICE.

There must be physics engines that can handle it as a one dimensional problem.

We live in one big scattering matrix, a universe of incompatible interfaces.

https://en.wikipedia.org/wiki/Acoustic_impedance

 

[Juanda]

I don't know about physics engines but I'm fairly confident a problem like this could be solved with FEM analysis. It'd require solving the problem in the time domain which is often not included in the free versions of these kinds of software.

But how cool would it be to have an analytical simple solution for a case like this? It's just 2 bodies after all. How hard can it be?
It's always surprising to me how some problems are easy to state and easy to visualize but then the necessary math to solve it has to be summoned from the most obscure places.
I want the universe to bend to my current knowledge or maybe a little more so that it is still reachable with some effort and research. I don't think it's going to happen anytime soon though .

 

[Baluncore]

I want the universe to bend to my current knowledge or maybe a little more so that it is still reachable with some effort and research.

I agree.
It needs to be kept sufficiently difficult, so someone will pay small teams of co-dependent physicists to research it.
I think we are stuck with bending our current knowledge to better fit our physical universe.

I have seen the results from commercial hydraulic pipeline modelling systems that can identify time-domain water hammer, based on transmission line equations.

 

[Frabjous]

If you do this in 1d with square waves assuming linear elasticity, you can tease out some of the physics with impedance matching. You end up having to track a lot of waves because they keep doubling at the material interface due to transmission and reflection. It consists of algebraic calculations where the relevant parameters are “changes in velocity” and “density*sound speed” (impedance) of both materials.

 

[Juanda]

Is that really easier than just applying a constant force?
I don't know how to solve it either way but I'm curious.
I imagined it with a constant force from the beginning and then the waves would emanate by themselves due to the elasticity of the rod. But it's been already a few answers mentioning a wave as the input.

 

[Frabjous]

Is that really easier than just applying a constant force?
I don't know how to solve it either way but I'm curious.
I imagined it with a constant force from the beginning and then the waves would emanate by themselves due to the elasticity of the rod. But it's been already a few answers mentioning a wave as the input.

Waves are how the information that a force has been applied is transmitted to other locations. In this case, the pressure and velocity changes are transmitted via waves.

 

[Baluncore]

But it's been already a few answers mentioning a wave as the input.

The stimulation could be anything that fits your model. A constant force that first appears at time zero, and may turn off instantly, some time later. It could be a half cycle of sinewave, like a hammer blow. A frequency chirp, or a Dirac delta function.

Imagine the model for a bouncing diesel pile-driver, sinking piles into mud. What is the optimum hammer rate and jump height?
Where does all that energy go?

 

[Juanda]

Imagine the model for a bouncing diesel pile-driver, sinking piles into mud. What is the optimum hammer rate and jump height?
Where does all that energy go?

I actually have no intuition to derive what's the optimum rate in this case.
So the energy is being lost as friction between the ground and the piles' walls I believe.
Since it's a rythmic thing I assume the optimum case is when resonance is achieved.
If the input force on the pile is the absolute value of a sine, and the input resonates with the pile, maybe the pile will wiggle harder so it will go further into the ground?

 

[Juanda]

Waves are how the information that a force has been applied is transmitted to other locations. In this case, the pressure and velocity changes are transmitted via waves.

Oh yeah that's for sure. I guess I just got confused for a moment about what you both posted. I thought you suggested using a wave as the input because it'd simplify the study. I chose a constant force because I thought it'd be the simplest and I couldn't understand how a time dependent input would cause a simpler output.
It's clear now.

 

[Juanda]

I recently watched a video related to this thread. This is the kind of thing I was aiming at when creating it. I wanted to be able to mathematically reproduce that kind of behavior although I feel the necessary math is just too hard for me now.



I consider the whole video to be worth it but I chopped it at the point where it shows the results.