- #1
masteriti
- 2
- 0
Robert Braeunig has an great blog on rocket science here: http://www.braeunig.us/space/index.htm, and I've been trying to follow the math his piece on Orbital Mechanics.
I'm having trouble in particular following his description on Kepler's 2nd law, here's how he puts it:
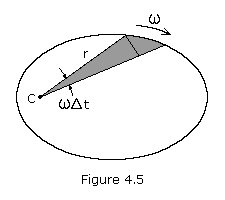
I understand the area of the triangle is given by (base x height)/2. I understand r is the triangle base in this case, but how does the opposite side equal rt or rωΔt?
The way I'm reading this is that Angular speed is just change in angle given a change in time ω = Δθ / Δt, so as I understand it, ωΔt just leaves the angle Δθ. So shouldn't the height then be r tan(Δθ)? What am I missing?
I'm having trouble in particular following his description on Kepler's 2nd law, here's how he puts it:
Figure 4.5 shows a particle revolving around C along some arbitrary path. The area swept out by the radius vector in a short time interval t is shown shaded. This area, neglecting the small triangular region at the end, is one-half the base times the height or approximately r(rt)/2. This expression becomes more exact as t approaches zero, i.e. the small triangle goes to zero more rapidly than the large one. The rate at which area is being swept out instantaneously is therefore
<br /> \lim_{t\rightarrow 0}{\Big[ \frac{r(rωΔt)}{2} \Big]} = \frac {ωr^2}{2}<br />
<br /> \lim_{t\rightarrow 0}{\Big[ \frac{r(rωΔt)}{2} \Big]} = \frac {ωr^2}{2}<br />
I understand the area of the triangle is given by (base x height)/2. I understand r is the triangle base in this case, but how does the opposite side equal rt or rωΔt?
The way I'm reading this is that Angular speed is just change in angle given a change in time ω = Δθ / Δt, so as I understand it, ωΔt just leaves the angle Δθ. So shouldn't the height then be r tan(Δθ)? What am I missing?
