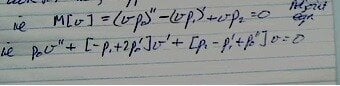- #1
nacho-man
- 171
- 0
So I have attached a screenshot of my lecturer's notes,
I can't quite understand the logical reasoning behind the link he's made between the two equations.
Previously he'd given us the fact that to check if an equation was adjoint,
you check if $ p_1' = p_0'' + p_2 $
for
$L = p_0u'' + p_1u' + p2u = r$
I am not sure if he has used this previous rule to here, but certainly I am a little dumbfounded.
I would appreciate any help!
Thanks
I can't quite understand the logical reasoning behind the link he's made between the two equations.
Previously he'd given us the fact that to check if an equation was adjoint,
you check if $ p_1' = p_0'' + p_2 $
for
$L = p_0u'' + p_1u' + p2u = r$
I am not sure if he has used this previous rule to here, but certainly I am a little dumbfounded.
I would appreciate any help!
Thanks