Help visualising this triangle

[charmedbeauty]

Homework Statement

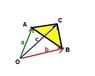
I think this must be really easy but I am not getting a visual for this triangle description.

Let ABC be a triangle with $\UparrowOA$=a and $/UparrowOB$=b and $/UparrowOC$ = c
Where O is the origin .

Homework Equations

The Attempt at a Solution

How can I have a triangle ABC where all A,B,C are sides coming from O

The way I'm looking at this is I have a point O, where the lines A,B,C start from ie, A,B,C only have one available endpoint.

So how can these lines make a triangle without introducing a new line??

Clearly, I am imagining things wrong here, I tried drawing it but it still didn't work. Help!

 

[ehild]

See attachment.

ehild

 

[charmedbeauty]

see attachment.

Ehild

thank you sir!

 

[charmedbeauty]

See attachment.

ehild

Hmm I have a question related to this triangle and it asks

i) If M is the midpoint of the line segment AB and P is the midpoint of the line segment CB express the vectors $\vec OM$ and $\vec OP$ in terms of a,b, and c.

ii) Show that $\vec MP$ is parallel to $\vec AC$ and has half its length.

Ok for part i) the answer is 1/2(b-a), 1/2(b-c), but to me it should be 1/2(b+a), 1/2(b+c)... as if you were to minus a or c does that not imply that you 'attach a/c to the end of vector b or in this case 1/2b and 1/2 (c,a)...
I think the difficulty I am having is understanding the direction in the vector, how do I know which way it is 'pointing' so to speak??

in this situation what would the addition of the vectors look like?

Thanks!

 

[Curious3141]

Hmm I have a question related to this triangle and it asks

i) If M is the midpoint of the line segment AB and P is the midpoint of the line segment CB express the vectors $\vec OM$ and $\vec OP$ in terms of a,b, and c.

ii) Show that $\vec MP$ is parallel to $\vec AC$ and has half its length.

Ok for part i) the answer is 1/2(b-a), 1/2(b-c), but to me it should be 1/2(b+a), 1/2(b+c)... as if you were to minus a or c does that not imply that you 'attach a/c to the end of vector b or in this case 1/2b and 1/2 (c,a)...
I think the difficulty I am having is understanding the direction in the vector, how do I know which way it is 'pointing' so to speak??

in this situation what would the addition of the vectors look like?

Thanks!

If your answer is that $\vec{OM} = \frac{1}{2}$(a + b) and that $\vec{OP} = \frac{1}{2}$(b + c),

then you are, in fact, right (and the book is wrong). a, b and c are position vectors - which means they define the positions of points A, B and C respectively with respect to a common origin O. By convention, they *always* point outward from the origin O toward the terminal point. So a = $\vec{OA}$, etc.

 

[charmedbeauty]

If your answer is that $\vec OM = \frac{1}{2}$(a + b) and that $\vec OP = \frac{1}{2}$(b + c),

then you are, in fact, right (and the book is wrong). a, b and c are position vectors - which means they define the positions of points A, B and C respectively with respect to a common origin O. By convention, they *always* point outward from the origin O toward the terminal point. So a = $\vec OA$, etc.

OK just wanted to clear that up yeah in the book the have 1/2(b-a),1/2(b-c)... thanks for the quick reply! Keep it ℝeal!