- #1
Khesahn
- 5
- 0
Homework Statement
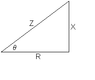
In a 60 Hz series RL network, the source is supplying 400 W of real power. If R = 15.08 Ω and L = 40 mH, find
a. The power factor. (Indicate if it is leading or lagging)
b. The apparent power supplied.
c. The reactive power supplied.
Homework Equations
None were given
The Attempt at a Solution
Ive been trying to google about power factor and reading up on it for quite some time, but I am still stuck. I know I can get PF by taking cosθ, but I am unsure of how to find θ for this particular problem. I believe it can be done by taking cos^(-1) (Real Power/Apparent Power), but again I was not sure of how to find apparent power.
I guess the biggest problem for me so far is been trying to relate the 60Hz to the rest of the problem. If someone could give me a hint on this I would greatly appreciate it. I had a funeral to attend to so I missed the class discussing most of these things, and its been difficult trying to read up on it online. Any help is appreciated!