- #1
Juanda
Gold Member
- 426
- 138
- TL;DR Summary
- Something does not click in my head about bolted joints.
I'm trying to understand bolted joints better. For reference, this is from Shigley’s.

Conceptually it makes total sense. And it is obviously right especially because it's in THAT book. But when I try to test it myself some contradictions appear and I can't understand what's happening.
First, during the preload process (a→b), the bolt and the clamped components work as springs in series. Is that correct? The same force ##F_i## is applied through them and they have different displacements. Although they are not in the typical physical configuration of springs in series (one spring after the other) I believe they fulfill the definition. Therefore, when applying ##F_i## the clamped parts are being compressed ##\delta_m## and the bolt is being elongated ##\delta_b## (Note that ##\delta_m \neq \delta_b## necessarily since they depend of the stiffness of each of the elements).
Then, during the loading process (b→c) the elements in the joint are working as springs in parallel because they have the same displacement. The displacements being ##\Delta \delta_m=\Delta \delta_b##.
I tested the formulas with some nonrealistic numbers to see if I could make sense out of the results. (I'm aware the formulas are only valid as long as gapping does not occur).
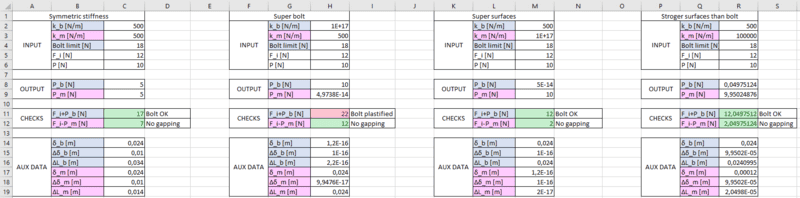
The case with the "super bolt" makes perfect sense. During the preload process with ##F_i=12N## the bolt will need to deform very little ##\delta_b \approx 0## to achieve the preload and the clamped parts will deform much more ##\delta_m \neq 0##. Then, when the separation load ##P## is applied, gapping is still very far because the load can be transmitted through the bolt without causing almost any deformation so the clamped force ##F_i-P_m \approx F_i## remains the same and the total load on the bolt is the preload plus the external load ##F_i+P_b \approx F_i+P##.
HOWEVER, the case with the "super surfaces" is causing me all kinds of headaches. Now, during the preload process, the bolt will deform significantly compared with the clamped parts which will remain almost undeformed. I have trouble understanding what's happening when the load is applied because I can't wrap my head around the fact that when I apply an external separating load ##P##, the tension on the bolt is almost unaffected. It makes sense that the remaining load in the joint is ##\approx F_i-P \approx 2N## but I don't understand why ##P## does not cause an increment in the tension in the bolt. The bolt is what is keeping the clamped parts together so this result feels incredibly counterintuitive to me.
I hope that by understanding these two extreme cases I'll be able to understand all the combinations in between. If there is something not correctly exposed in the post let me know of it and I'll try to be clearer.
Thanks in advance.
PS: By the way, I can share the Excel so you can see the formulas in each cell in case you want to check them but I saw in a different thread that Excel files can contain malware so mods prefer to keep them out of the forum. If you want the file and there is an alternative method to get it to you tell me how and I'll share it.
Conceptually it makes total sense. And it is obviously right especially because it's in THAT book. But when I try to test it myself some contradictions appear and I can't understand what's happening.
First, during the preload process (a→b), the bolt and the clamped components work as springs in series. Is that correct? The same force ##F_i## is applied through them and they have different displacements. Although they are not in the typical physical configuration of springs in series (one spring after the other) I believe they fulfill the definition. Therefore, when applying ##F_i## the clamped parts are being compressed ##\delta_m## and the bolt is being elongated ##\delta_b## (Note that ##\delta_m \neq \delta_b## necessarily since they depend of the stiffness of each of the elements).
Then, during the loading process (b→c) the elements in the joint are working as springs in parallel because they have the same displacement. The displacements being ##\Delta \delta_m=\Delta \delta_b##.
I tested the formulas with some nonrealistic numbers to see if I could make sense out of the results. (I'm aware the formulas are only valid as long as gapping does not occur).
The case with the "super bolt" makes perfect sense. During the preload process with ##F_i=12N## the bolt will need to deform very little ##\delta_b \approx 0## to achieve the preload and the clamped parts will deform much more ##\delta_m \neq 0##. Then, when the separation load ##P## is applied, gapping is still very far because the load can be transmitted through the bolt without causing almost any deformation so the clamped force ##F_i-P_m \approx F_i## remains the same and the total load on the bolt is the preload plus the external load ##F_i+P_b \approx F_i+P##.
HOWEVER, the case with the "super surfaces" is causing me all kinds of headaches. Now, during the preload process, the bolt will deform significantly compared with the clamped parts which will remain almost undeformed. I have trouble understanding what's happening when the load is applied because I can't wrap my head around the fact that when I apply an external separating load ##P##, the tension on the bolt is almost unaffected. It makes sense that the remaining load in the joint is ##\approx F_i-P \approx 2N## but I don't understand why ##P## does not cause an increment in the tension in the bolt. The bolt is what is keeping the clamped parts together so this result feels incredibly counterintuitive to me.
I hope that by understanding these two extreme cases I'll be able to understand all the combinations in between. If there is something not correctly exposed in the post let me know of it and I'll try to be clearer.
Thanks in advance.
PS: By the way, I can share the Excel so you can see the formulas in each cell in case you want to check them but I saw in a different thread that Excel files can contain malware so mods prefer to keep them out of the forum. If you want the file and there is an alternative method to get it to you tell me how and I'll share it.
Last edited:
