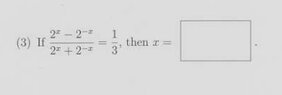squexy
- 18
- 0
Could you help me with this questions as well?
View attachment 3751This is what I have done:
2^x - 2^-x/ 2^x +2^-x
2^x - 1/2^x/ 2^x +1/2^x
u -1/u/u+1/u =1/3
3u² - 3/ 3u² +3= U
u² - 1- u = 0
u² - u - 1 =0
(u -1) (u+1) =0
U =1 or -1
View attachment 3751This is what I have done:
2^x - 2^-x/ 2^x +2^-x
2^x - 1/2^x/ 2^x +1/2^x
u -1/u/u+1/u =1/3
3u² - 3/ 3u² +3= U
u² - 1- u = 0
u² - u - 1 =0
(u -1) (u+1) =0
U =1 or -1