chessguy103
- 13
- 3
Hi all,
I'm working on designing a device, and I'm having trouble with material selection for a shaft, modeled below.
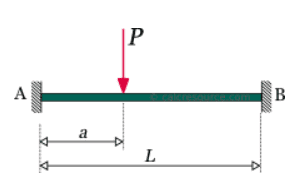
I have found the maximum stress due to bending on the shaft in question by using
I got σ = 31.2 MPa. This is where I'm stuck. Now that I have this stress, how do I choose a material? Do I just look at yield strength?
Any help is appreciated. Thanks :)
I'm working on designing a device, and I'm having trouble with material selection for a shaft, modeled below.
I have found the maximum stress due to bending on the shaft in question by using
σ_max = (M_max*y)/I
where σ is stress, M is bending moment, y is distance from the neutral axis (aka radius of shaft), and I is polar moment of interia.I got σ = 31.2 MPa. This is where I'm stuck. Now that I have this stress, how do I choose a material? Do I just look at yield strength?
Any help is appreciated. Thanks :)