- #1
spider853
- 2
- 0
Hi, I've started to write a simulator for SPH, and I'm fallowing a paper on SPH simulation,
The problem is that in that paper they show the formulas for computing force but they don't tell you on what vector do you need to apply this force.
So here are the formulas for pressure, viscosity and tension:
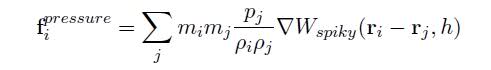
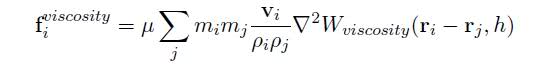
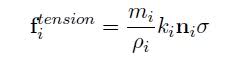
as you can see they return scalars. but I need vectors (2D or 3D) so I can apply it to the acceleration.
I suppose they are related to unit vector between the current particle and the neighbor particle (^rij)
but not sure if I need to sum or scale it...
Thanks
The problem is that in that paper they show the formulas for computing force but they don't tell you on what vector do you need to apply this force.
So here are the formulas for pressure, viscosity and tension:
as you can see they return scalars. but I need vectors (2D or 3D) so I can apply it to the acceleration.
I suppose they are related to unit vector between the current particle and the neighbor particle (^rij)
but not sure if I need to sum or scale it...
Thanks