RahSuh
- 10
- 4
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: Am stuck on an integral at the bottom of page 34
Hi - I am working thru (by myself) the small textbook by Bohn on Analytical Mechanics. Its very good but am stuck on Page 34, at the bottom. It concerns the "action" of a simple pendulum - I understand the math concept of action as Bohn . I just dont understand how he gets the integral works. ie in the snip attached how he gets from the first line of the integral for A to the second line. The integral looks really, really messy. Any help appreciated. (the book is very, very good - so far!)
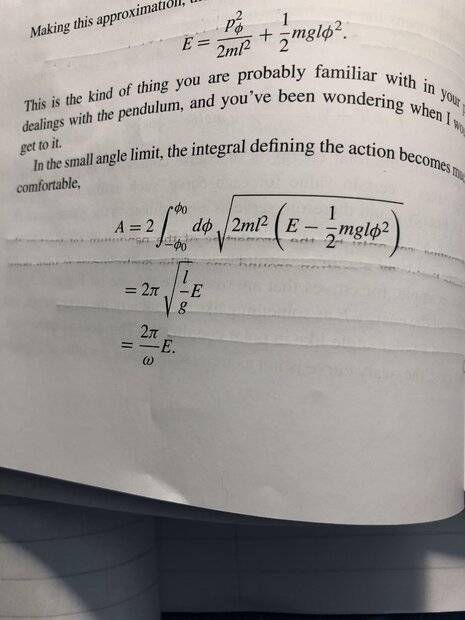
Hi - I am working thru (by myself) the small textbook by Bohn on Analytical Mechanics. Its very good but am stuck on Page 34, at the bottom. It concerns the "action" of a simple pendulum - I understand the math concept of action as Bohn . I just dont understand how he gets the integral works. ie in the snip attached how he gets from the first line of the integral for A to the second line. The integral looks really, really messy. Any help appreciated. (the book is very, very good - so far!)
Last edited by a moderator: