- #1
hgphtgi
- 12
- 0
Hello Gys
I have new question for you today... if u ready, let's begin
http://www.mediafire.com/view/?2pp4u074ppijfbt
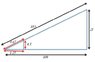
we have two triangles, the main one is the blue the secondary is the red.
if we divide the main triangle into two triangles we will get
The red triangle a=1.25, b=4.5 and c=4.67
The new triangle will be a=100-1.25=98.75, 25-4.5=20.5 so c=sqrt((98.75)^2+(20.5)^2) ===> c=100.85
===========================
Now we have two triangles
1- a=1.25, b=4.5 and c=4.67
2- a=98.75, b=20.5 and c=100.85
The question is there is some thing missing because when we want to combine the two triangles again suppose we get same length's of the the main triangles ( blue triangles ).
Any one could get the point ??
Tnx all
I have new question for you today... if u ready, let's begin
http://www.mediafire.com/view/?2pp4u074ppijfbt
we have two triangles, the main one is the blue the secondary is the red.
if we divide the main triangle into two triangles we will get
The red triangle a=1.25, b=4.5 and c=4.67
The new triangle will be a=100-1.25=98.75, 25-4.5=20.5 so c=sqrt((98.75)^2+(20.5)^2) ===> c=100.85
===========================
Now we have two triangles
1- a=1.25, b=4.5 and c=4.67
2- a=98.75, b=20.5 and c=100.85
The question is there is some thing missing because when we want to combine the two triangles again suppose we get same length's of the the main triangles ( blue triangles ).
Any one could get the point ??
Tnx all
Attachments
Last edited by a moderator: