Help with understanding a Friedmann flat universe

[Cerenkov]

Hello.
I've been doing some reading about Friedmann's three types of GR solution that yield closed, open and flat universes. I think I can grasp the closed solution best. As far as I understand it a closed universe is finite in both time and space. It begins, grows and then collapses in upon itself, taking time to do these things. I also realize that the volume of space is represented, not by the interior of the sphere below, but by it's surface area. That area grows, reaches a maximum size and then shrinks. I think I also see how such a universe is unbounded. Just as an ant would never come to any kind of edge when crawling over the surface of a sphere, so a spaceship would never come to any kind of edge of a closed universe. It could (theoretically) travel forever, with it's occupants never realizing that the volume they are traversing is actually finite. So far (I hope) so good.

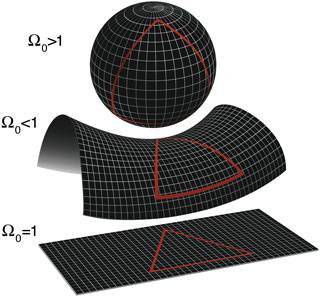
But the open and flat universes are where I need some help. Please!
The books and internet articles I've read tell me that these two types of universe are considered to be infinite. I've also read that our universe has been found to be flat, to a reasonable degree of confidence. That being so, in my mind I picture the rectangular grid representing a (our?) flat universe extending forever, without any kind of boundary or edge. Infinite meaning without end.

However, I'm still struggling on a number of points and would appreciate some help - preferably in a non-technical and easy-to-grasp way. I'll list them below, but please be patient with me if I phrase them awkwardly, wrongly or naively. Thank you.

1.
As explained above I think I can visualize how a closed Friedmann universe evolves over time. But am I right in thinking that all three solutions have something like a definite moment of origin? If not can what is theorized to happen be be explained to me please?

2.
If there is a moment of origin (T = 0?) that applies to all three solutions, then do the open and flat universes become infinitely-large over time or are they considered to be infinitely-large from get go?

3.

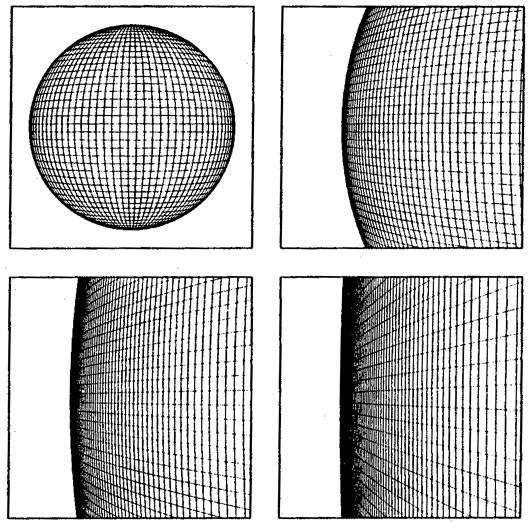
I've seen the above diagram used to represent how inflation might 'flatten' our universe and give it the appearance of being flat. It's my understanding that this process happens over time. But wouldn't that mean that the volume of space is actually finite - not unlike the finite but unbounded volume of a Friedmann closed universe?

4.
If I'm barking up the wrong tree here (i.e., flat and open universes are infinite from get go) then could somebody please explain this to me in a way that I can understand? I ask because I just don't get how the evolution of these two types of universe satisfy what seem to me to be two, mutually-exclusive conditions. How can our infinitely-large and flat universe originate from something infinitely-small (the initial singularity) without transitioning from one condition to the other over time?

I can see how a closed universe does this, because the volumes involved are finite and they evolve over time.

But infinitely large from infinitely small in zero time?

Thanks for any help (on my basic level) given.

Cerenkov.p.s.
Yes, I have read that there are some kinds of infinities that are larger than others and that infinities can also grow. (Hilbert's Hotel?) So I do get that. But this growth would, as far as I naively understand it, happen over time. It's the jump from zero size to infinite size in zero time that's throwing me!

 

[Orodruin]

As far as I understand it a closed universe is finite in both time and space. It begins, grows and then collapses in upon itself, taking time to do these things.

This is not completely correct. In particular, you can have a spatially closed universe that expands forever if there is a sufficient amount of dark energy. Note that what you are shown in those pictures are spatial hypersurfaces, not spacetime itself.

1.
As explained above I think I can visualize how a closed Friedmann universe evolves over time. But am I right in thinking that all three solutions have something like a definite moment of origin? If not can what is theorized to happen be be explained to me please?

Only if you try to extrapolate the solution back using known and well established physics do you end up with a "singularity". Most physicists believe that our knowledge of physics breaks down much before that. Inflation is a very popular idea for trying to describe what happened before the standard Big Bang. It is still unverified however.

2.
If there is a moment of origin (T = 0?) that applies to all three solutions, then do the open and flat universes become infinitely-large over time or are they considered to be infinitely-large from get go?

They would be infinitely large from the beginning.

I've seen the above diagram used to represent how inflation might 'flatten' our universe and give it the appearance of being flat. It's my understanding that this process happens over time. But wouldn't that mean that the volume of space is actually finite - not unlike the finite but unbounded volume of a Friedmann closed universe?

It would flatten also an open universe. The point is that it would make the universe so close to flat that it would be essentially impossible for us to realize that it is not flat.

 

[PeterDonis]

Inflation is a very popular idea for trying to describe what happened before the standard Big Bang.

Just to clarify, "the standard Big Bang" here does not (I assume) mean "the initial singularity". It means, roughly, "the hot, dense, rapidly expanding state that is the earliest for which we have good evidence and a good theoretical model of how the universe got from there to the way it is now".

 

[Orodruin]

I assume

You assume correctly. Good clarification.

 

[Cerenkov]

Thanks very much for the responses!

Ok, re question 3, I now see that it's impossible for us to tell by observation if our universe is actually flat or has been flattened by inflation.

As far as question 2 goes, if open and flat universes are considered to be infinitely large from their very beginnings, then how about this?
Rather than growing from a single point of origin (as is often and somewhat unhelpfully, shown in diagrams) would it be better to envisage all points of the space-time metric inflating equally and moving away from each other, equally? That way there is no edge and no center to deal with. The universe is then unbounded and all points or regions are alike. The universe would then be homogeneous and isotropic, wouldn't it? And this would fit with our observations of the recession of other galaxies? They appear to be receding from us but are actually receding from each other - once again doing away with any need to consider an edge or center? If I'm on the right track, then would what I've read about inflation solving the Horizon problem also be related to this notion?

For the record, I realize that inflation remains unverified. As I recall, the smoking gun for that would be the B-mode polarization of the CMB - which the Bicep-2 team thought they'd bagged? Or are there other lines of evidence that might do the job?Re those images of the spatial hypersurfaces (lifted from the NASA WMAP site)...
Yes, they aren't space-time itself. But isn't it a reasonable analogy to say that they are representations of the space-time metric? Perhaps a bit like the contour lines on a map? The map itself isn't the actual surface of the terrain, but the contour lines allow us to gain a degree of understanding about the nature of the terrain?

Thanks again to Orodruin and PeterDonis.

Cerenkov.

 

[Orodruin]

That way there is no edge and no center to deal with. The universe is then unbounded and all points or regions are alike. The universe would then be homogeneous and isotropic, wouldn't it?

Yes. That the Universe is homogeneous and isotropic is the basic assumption behind the FLRW universe. It should therefore come as no surprise that the three geometries that result are homogeneous and isotropic. The only reason the images you find have boundaries is that it is impossible to draw an infinite plane.

But isn't it a reasonable analogy to say that they are representations of the space-time metric?

No. The spacetime metric relates to 4-dimensional spacetime. What those images represent are the shapes of the purely spatial hypersurfaces of constant cosmological time. Note that the notion of the curvature of space (not spacetime) depends on the type of foliation of spacetime that you make. See my Insight on coordinate dependent statements in an expanding universe.

 

[Cerenkov]

Cerenkov said: ↑
That way there is no edge and no center to deal with. The universe is then unbounded and all points or regions are alike. The universe would then be homogeneous and isotropic, wouldn't it?Yes. That the Universe is homogeneous and isotropic is the basic assumption behind the FLRW universe. It should therefore come as no surprise that the three geometries that result are homogeneous and isotropic. The only reason the images you find have boundaries is that it is impossible to draw an infinite plane.Thanks Orodruin.
This basic assumption of the FLRW is supported by what lines of evidence? The measurements of our universe's 'flatness' using the CMB? That's one that I know of. Are there any others?

Also, when it comes to homogeneity, don't the Hubble Deep fields (North and South) suggest that our universe is statistically similar in different directions and therefore, most likely, homogenous all over?

Lastly...Yes, I see what you mean about the boundaries in the images. Thank you.

C.

 

[Cerenkov]

Cerenkov said: ↑
But isn't it a reasonable analogy to say that they are representations of the space-time metric?No. The spacetime metric relates to 4-dimensional spacetime. What those images represent are the shapes of the purely spatial hypersurfaces of constant cosmological time. Note that the notion of the curvature of space (not spacetime) depends on the type of foliation of spacetime that you make. See my Insight on coordinate dependent statements in an expanding universe.Thanks again, Orodruin.
I must give your comments more thought and come back to you. For the record, please let me state that my level of understanding of these things is... basic. So please bear with me. Also, let me assure you that my interest in these things is genuine. I'm not trying to waste your time here. It's just that there's a mismatch between my desire to understand more and my ability to do so.

Perhaps I'm a bit like Salieri in 'Amadeus'? He eagerly wanted to compose beautiful music like Mozart, but lacked the talent to do so. In a similar way, I eagerly want to understand more about cosmology, but lack the skill to do so.

Thanks,

C.

 

[phinds]

@Cerenkov I recommend that article linked to in my signature. It offers statements without proof or evidence but they are supported by evidence and represent what, I think, you already understand about the expanding universe, perhaps with some clarifications of ways in which some descriptions are wrong or misleading.

 

[PeterDonis]

would it be better to envisage all points of the space-time metric inflating equally and moving away from each other, equally?

Not of the spacetime metric, no. Points in spacetime are points in space and time. Spacetime does not expand, inflate, or change. It already contains within its 4-dimensional geometry the entire history through time of everything in space.

If you adopt particular coordinates (the ones used in the standard Friedmann-Robertson-Walker coordinate chart), then you can view points of space as moving away from each other equally, with respect to the time coordinate. This amounts to taking the 4-dimensional spacetime geometry and slicing it into an infinite "stack" of 3-dimensional spaces, indexed by the time coordinate. For the open and flat cases, each of the 3-dimensional spaces are infinite, and if we keep track of particular "points in space" (often this is described as picking out a set of observers, called "comoving observers", who all see the universe as homogeneous and isotropic, and treating each one of them as marking out a particular point in space), we find that they are moving apart with time as we travel up (i.e., in the direction of increasing time) the infinite stack of 3-dimensional spaces.

 

[PeterDonis]

This basic assumption of the FLRW is supported by what lines of evidence? The measurements of our universe's 'flatness' using the CMB?

The key property of the CMB, for this purpose, is not that it provides a measurement of the universe's flatness, but that it provides a measurement of the universe's isotropy--being the same in all directions. The CMB is isotropic to about one part in a hundred thousand; that's a very high degree of isotropy.

 

[George Jones]

The key property of the CMB, for this purpose, is not that it provides a measurement of the universe's flatness, but that it provides a measurement of the universe's isotropy--being the same in all directions. The CMB is isotropic to about one part in a hundred thousand; that's a very high degree of isotropy.

And this very small anisotropy provides fairly strong evidence that spatial curvature is quite small and experimentally consistent with spatial flatness.

 

[George Jones]

And this very small anisotropy provides fairly strong evidence that spatial curvature is quite small and experimentally consistent with spatial flatness.

Actually a little more than the angular sizes of the anisotopies is needed, e.g., the CMB anisotropies and an independent measurement of the Hubble parameter.

 

[timmdeeg]

And this very small anisotropy provides fairly strong evidence that spatial curvature is quite small and experimentally consistent with spatial flatness.

To my knowledge this measurement is based on the sum of the angles of a triangle, whereby one side of the triangle is the known length then (time of last scattering) of the first acoustic peak. The angle under which we see this peak today is about 1°. But if I see it correctly this triangle lies on a hyperplane. How can one perform the measurement with light emitted then and received today?