Help with unit vector for a magnetic field

[guyvsdcsniper]

Homework Statement:

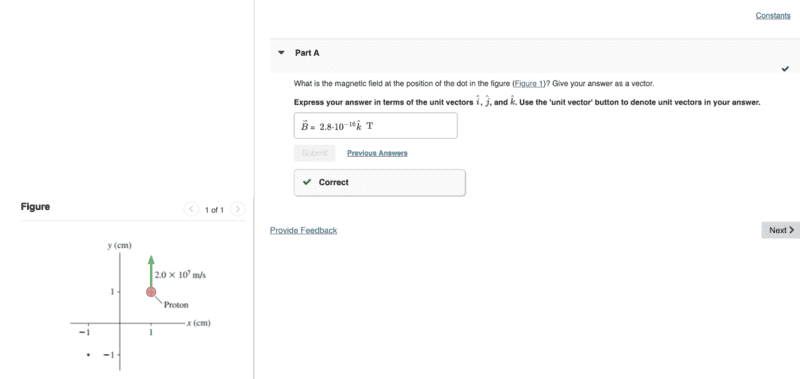
What is the magnetic field at the position of the dot in the figure?

Relevant Equations:

Cross Product

So when evaluation the cross product of the velocity of the charge and the unit vectors associated with the point I am getting

v x r = j x [ i + j].
Well j x j is 0.
j x i = -k, but yet the answer is positive. Why is this?

 

[Orodruin]

The vector r is the position of the point relative to the proton, not the position of the proton.

 

[kuruman]

Why should there be a magnetic field? What is given in this problem that you did not include in the Homework Statement and is not shown in the picture you posted? We are not even told the sign of the charge.

 

[Orodruin]

Why should there be a magnetic field? What is given in this problem that you did not include in the Homework Statement and is not shown in the picture you posted? We are not even told the sign of the charge.

The picture shows a proton at (1,1) with a given velocity and asks for the magnetic field at (-1,-1). It seems pretty clear to me.

 

[kuruman]

The picture shows a proton at (1,1) with a given velocity and asks for the magnetic field at (-1,-1). It seems pretty clear to me.

Yes, I see that now that I switched browsers.

 

[SammyS]

Yes, I see that now that I switched browsers.

Yes, I agree that we can figure out the problem which likely is to be solved.

However, I agree with your previous post in that a clear problem statement would be a great help. Especially one written as text and readable with any browser.