- #1
kidd
- 15
- 0
Help!A question very difficulty!
The question is:
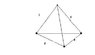
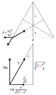
Three identical small spheres of mass m are suspended by threads of negligible masses and equal length L from a common point.Acharge Q is divided equally between the spheres and they come to equilibrium at the coners of a horizontal equilateral triangle whose slides are d.
Prove the following Q²=12x∑mgd³[L²-d²/3]^-1/2.
P/S:No figure given,need draw myself!Any one know it,pls help me...
The question is:
Three identical small spheres of mass m are suspended by threads of negligible masses and equal length L from a common point.Acharge Q is divided equally between the spheres and they come to equilibrium at the coners of a horizontal equilateral triangle whose slides are d.
Prove the following Q²=12x∑mgd³[L²-d²/3]^-1/2.
P/S:No figure given,need draw myself!Any one know it,pls help me...