Herodotus Machine: Tilting & Force Calculation

[adapterant]

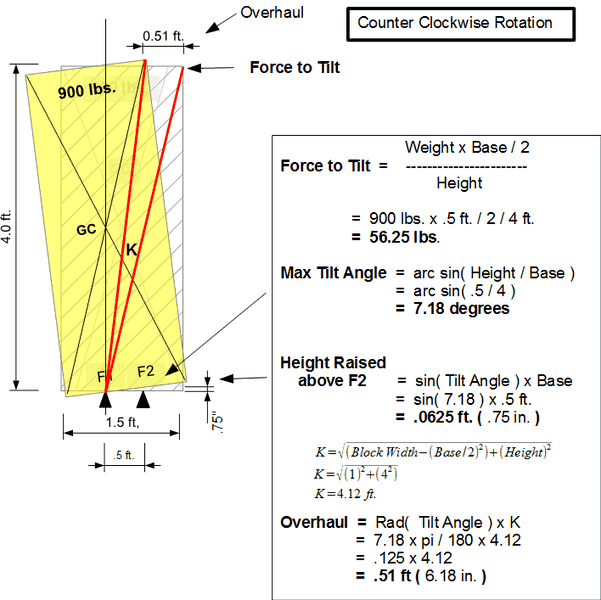
I started looking into the operation of a really simple machine called the "Herodotus Machine". A quick Google search gives some good info on it https://www.google.com/webhp?sourceid=chrome-instant&ion=1&espv=2&ie=UTF-8#q=Herodotus+Machine . I wanted to use a block that was taller than it was wide and determine first what force would be needed to tilt it from a level position to its tipping point. Here is my work on the counter clockwise rotation of the block.

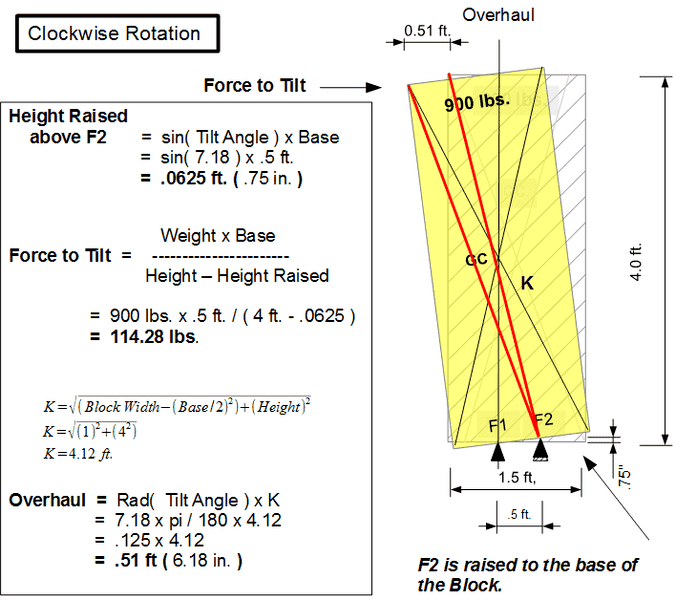
Tilting it back to a level position requires more force and below is what I believe is a correct for calculating that force, moving the block in a clockwise direction.

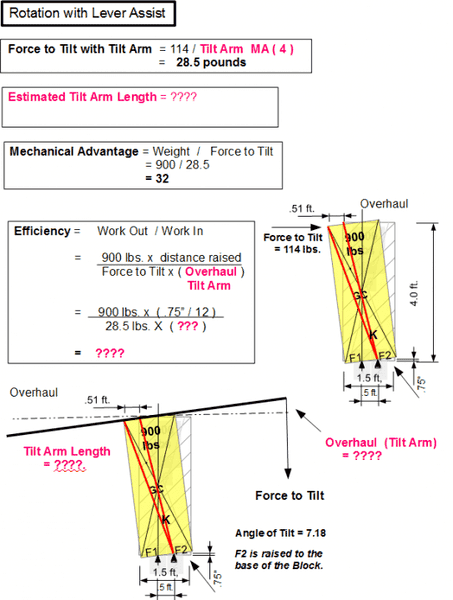
What has perplexed me is how to calculate this action when one uses a cross beam, across the top of the block, to tilt it back and forth. I would sure appreciate some help in solving the missing values in the next image. I set the Mechanical Advantage provided by the cross beam to 4. The missing values I'd like to come up with are in red. One point to consider, does the height of the block make any difference in the calculation. If it doesn't, then the force needed to tilt in the previous examples are irrelevant. If that is the case then what would be the force needed to tilt the block from a level position and from a tilted position with a beam that could provide a MA of 4.

 

[Simon Bridge]

You diagrams do not follow the designs in the links provided.
Rocking the block to raise it woul work better, and easier to model, if you use levers from the bottom.
Instead of a force-based analysis, try work and energy.

 

[adapterant]

Simon, thanks for taking note. That link shows what has been considered to be the original design from way back. I didn't make that video. They did a pretty good job though.
I believe that I have come up with a solution to my problem. I thought that the Mechanical Advantage that the block exhibited when being pushed from its top, as shown in the 1st and 2nd drawings, added to the overall MA when the Tilt Lever was added. As it turns out the height of the block only serves to carry mass (weight). The following is correct I believe and gives the main items I was looking for:

Force to Tilt x Length x cos(Tilt Angle) = Weight x (F1 to F2)

Length = ( 900 pounds x .5 ) / 28.5 pounds x cos( 7.14 )

Length = 15.9 feet.

Total Length = 2 x 15.9 ft. + ( F1 to F2 )

= 32.3 feet

And you could have this top or bottom of the block. I guess it would depend on how you wanted to remove the block from the machine once it was to the height you wanted.

 

[Simon Bridge]

The link top of post #1 is to a google search page.
Most of the search results show a ramp and lever arrangememt, with holes in the ramp.
It looks like you are thinking of rocking the block while inserting chocks.

You would not really want to upend the block for lifting by this method... its less stable that way, even if tall blocks are usually easier to rock.

 

[adapterant]

My bad, the link is a look at more than one version of what could be a Herodotus Machine. I was trying to examine the one where the block is tilted up and a short wood piece is slid under it. and it is really any ones guess that this is a more accurate version than any other. Herodotus didn't leave a lot to go on.

 

[Simon Bridge]

To get the benifit of adding a beam to your setup, you need it upright rather than across the top.
You appear to be doing thevanalysis by rule... try using physics instead.

 

[adapterant]

Yes, placing the beam upright along the side does give one additional leverage when tilting.