Hidden phase in polarization tests of Bell's inequality?

[Leureka]

TL;DR Summary

Can a phase property explain violation of bell's inequality?

Hi there, i must preface with saying my understanding of the problem is limited to undergraduate quantum mechanics, since my spacialization is chemistry. I know the basic principles, like hilbert spaces, vector bases etc... I'm only asking this question because i genuinely want to understand where my thinking goes wrong.

I'm struggling to completely wrap my head around Bell's tests with polarization of photons. Popular videos always explain this with showing very simple tables of possible measurement outcomes, with a net probabilty for each photon passing being proportional to the square of the cosine of the angle between polarizers (Malus' law, basically), and showing how this probability distribution is fundamentally incompatible with hidden variables on each photon, determining beforehand wether it will pass or not.

It is my understanding that each time a photon arrives at one of the detectors, there is fundamentally a 50/50 chance the detector will blip or not. It is only when I combine my results with those from the other detector that i will see there actually is a correlation between the results, and this will depend on the angle between the detectors, which on a surface level seems spooky because how can each photon know what the other photon did, as to preserve the correlations?

For example, for angles at 22.5 degrees there is an overall 85% correlation. Which means, in a set of 10 measurements, around 8 of them will be the same, even though at each detector the total distribution is 50%, like in the image below.

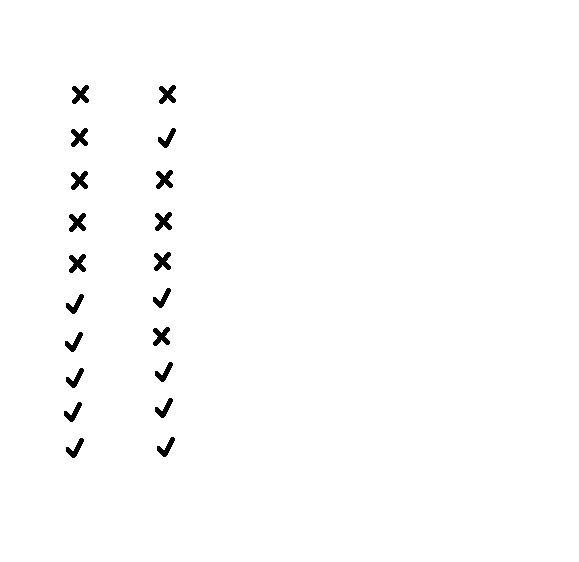
But here's an explanation which involves entirely local variables that can come up with the exact same distribution.
Imagine a vector in a circle. With respect to the horizontal, this vector can take on any angle from 0 to 360 degrees. This can represent some kind of hidden phase the two entangled photons have in common (in the image below, one is colored yellow and another is red; these are just different independent vectors, as if they were on different pairs of photons).

Now what happens at the moment of measurement? There is an angle choice, but no matter what this angle choice is, there will always be a 50% chance to measure the photon. I represented this by coloring half the circle in blue. If the phase vector lands inside the blue area, the detector will blip. What the angle choice does, is rotate the circle. The phase vector is invariant, but it has a definite inclination with the respect to the measurement angle, which is simply the horizontal cutting the circle in two.
The only nuance is that the angle inclination is not linear: so at 0 degrees the two horizontals are the same, but at 45 degrees the horizontal are perpendicular, at 22.5 it is at 15 degrees from the horizontal, and so on. The important point is that the probability is given by the overlap of the blue areas. (note that here the 22.5 is not the correct angle only for ease of drawing)

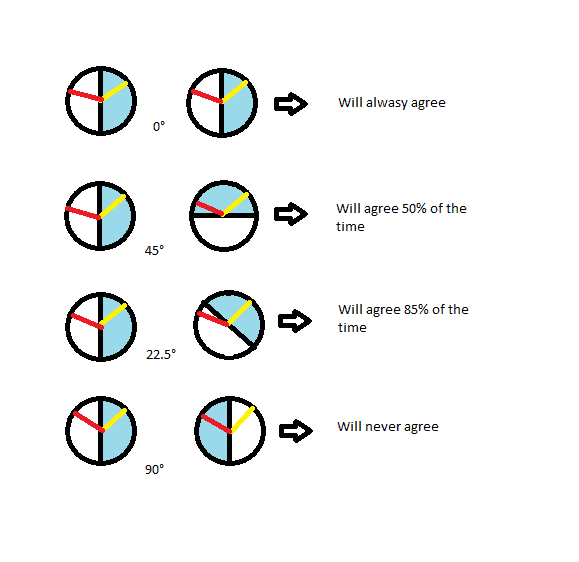
There is clearly nothing spooky in this setup. The only issue is that it's not clear to me what the circle actually represents, but whatever it is it is a property of the detector, which is nonlinear but still local. From the looks of my diagram, it seems as if the detectors also have a certain "phase", and interaction only happens when both phases are compatible. Here I chose to picture the phase of the first detector always the same for simplicity, but you could rotate it and still get the same result (if you also rotate the other circle by the same amount, which is akin to keeping the angle difference the same). In this sense there is no absolute detector phase, the only constraint is that they must be the same for polarizers at the same angle, which makes sense since they should be, in principle, indistinguishable. As for the non-linearity, I havent really thought too much on how to explain that away, but it eerely reminds me of the relationship between quaternions, which is also non-linear. Here's another analogy: replace the two circles with two ellipses. Now rotate one. The overlap is not linear anymore (see below). An ellipse in general does not reproduce a cosine dependence, but you can just pick a shape that will, it's a matter of geometricizing the problem imho.

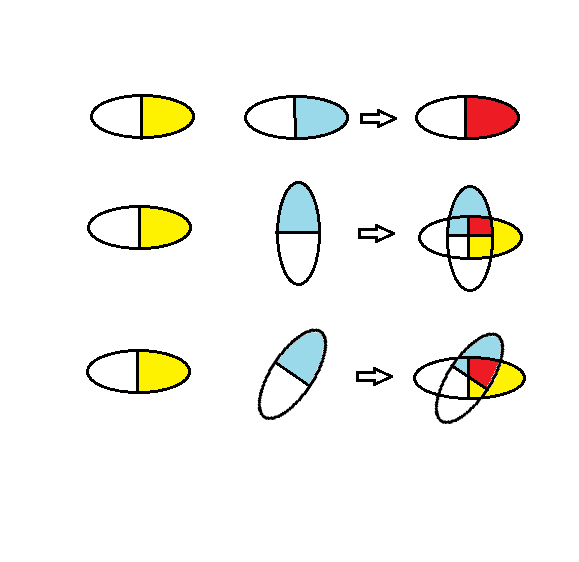
Here, the red area represent the overlap between the two ellipses. As you can see, it does not decrease linearly as the ellipse rotates.

In essence, the correlations are an interplay between the state of the photons and the state of the detector.

Comments anyone? Where did i go wrong? Are my assumptions incorrect for example? Did I misunderstand experimental results?

 

[PeroK]

Bell's inequality assumes only the properties of classical probabilities. If that's wrong, then there would have to be something wrong with his mathematics, regarding elementary probability theory.

 

[PeroK]

That said, if you correlate the detector with the particles, then I guess any correlation is possible. I think that's the basis of sone superdeterministic theories.

 

[WernerQH]

The important point is that the probability is given by the overlap of the blue areas. (note that here the 22.5 is not the correct angle only for ease of drawing)

I think a more careful drawing would help. The overlap varies linearly with the angle, leading to a triangular graph that always falls below the cosine law that was found experimentally (and was predicted by QM, of course). The (anti-)correlations are stronger than what simple local models can produce.

 

[Cthugha]

This indeed is the best classical approximation there is, but it still does not match the experimental predictions. Below, I uploaded two figures from my quantum optics lecture which discuss exactly that question (sorry for the German). It considers an entangled photon pair of opposite polarization. The horizontal axis provides the relative angle between the detector polarizer settings. The measurement result is +1, if both detectors do the same thing (both detect a photon or both do not detect a photon) and -1 if both detectors do a different thing. The vertical axis is the mean value for this measurement result. The second figure shows the "detection" and "no detection" ranges for the relative angle between polarization and detector setting.

The red line is the classical hidden value result assuming Malus' law. This is as expected.

The blue one is a "disk" detection model (+ polarization as a hidden variable), which does what you describe. It fires all the time if the polarization (or the phase in your model) is within 45 degrees of the detector setting (or the detector setting +180 degrees of course) and does not fire otherwise. In that case, the detection probability is only given by the overlap given by the "disks" describing the angles. In that case you indeed get full correlation and full anti-correlation. However, this necessarily gives you a linear correlation curve as the overlap is obviously a linear function.

The black line gives you the quantum-mechanical description, which is obviously cos-like. As you can see, the curves agree for 0 and 90 degrees, but are most different for 22.5 and 67.5 degrees. If you have a look at Aspects's first paper, these are exactly the angles he used for the measurements. In my lecture, I usually discuss this detector model to motivate Aspect's choice of angles.

 

[Leureka]

I think a more careful drawing would help. The overlap varies linearly with the angle, leading to a triangular graph that always falls below the cosine law that was found experimentally (and was predicted by QM, of course). The (anti-)correlations are stronger than what simple local models can produce.

Not if you vary the angle non-linearly, as i explained further below in the post.

 

[WernerQH]

Not if you vary the angle non-linearly, as i explained further below in the post.

Twice the angle between the detectors? I'd still call that a linear relation.

 

[Leureka]

Twice the angle between the detectors? I'd still call that a linear relation.

No, it would be 0 when the angle difference is 0, less than 45 when 22.5 (i'd have to pull out pen and paper to get the actual real angle, but on my phone rn), 90 at 45, more than 135 at 67.5 and finally 180 at 90. Just vary the angle so that the overlap is correct. I don't see any fundamental principle why a variable couldn't vary this way, for example the arc length of an ellipse is not linearly correlated with the angle. But I might be wrong.

 

[WernerQH]

You would need to know the orientations of both detectors to choose the correct angle. Then it's no longer a "local" procedure that applies to each detector individually. You can produce any probability distribution with such contrivances.

 

[Leureka]

Here's another analogy: replace the two circles with two ellipses. Now rotate one. The overlap is not linear anymore. An ellipse in general does not reproduce a cosine dependence, but you can just pick a shape that will, it's a matter of geometricizing the problem imho.

@WernerQH EDIT: i thought more about your reply, and i concluded that in this setup, no, you don't need to know the orientation of both detectors. You can always tell whether the hidden phase of the photon lies inside the blue area on your detector (because it blips), but you can't know the detector phase orientation with respect to the other detector until you compare measurements. Which is what the experiment is actually telling us. When we compare results, we cross check polarizers and so we determine their phase correlation (how one circle, or ellipse, or whatever geometry explains the cosine dependence, is rotated with respect to the other). The photon correlation is a consequence of those particular, independent detector phase choices, but there is nothing in the photon that changes after measurement; only our knowledge of the system changes.

 

[DrClaude]

How does your idea work when there are three possible angle detectors?

 

[Leureka]

How does your idea work when there are three possible angle detectors?

As in? Sorry I'm only familiar with the polarizer and spin experiments. In the spin measurement experiment you have 3 detectors on each side, but only one at a time ever blips so the idea here should work just the same, with the only difference that you always measure a spin in both. The point is to look at the correlations where spins are opposite or not instead of whether a photon passed the polarizer or not (at least that's how i understood it), but the graphical representation here shouldn't differ.

 

[PeterDonis]

In essence, the correlations are an interplay between the state of the photons and the state of the detector.

As far as I can tell, this is still a local hidden variable model and therefore cannot produce violations of the Bell inequalities.

 

[Leureka]

This is still a local hidden variable model and therefore cannot produce violations of the Bell inequalities.

I knew that much. The thing is correlations in this model are those of the violations. This criticism really tells me nothing about what i got wrong.

 

[PeterDonis]

I knew that much.

Actually, on taking another look, I have changed my mind. Consider this key statement:

The important point is that the probability is given by the overlap of the blue areas.

The overlap of the blue areas is not a local quantity: it depends on the settings of both detectors, not just one. See @WernerQH's comment in post #9.

 

[Leureka]

Actually, on taking another look, I have changed my mind. Consider this key statement:The overlap of the blue areas is not a local quantity: it depends on the settings of both detectors, not just one. See @WernerQH's comment in post #9.

Right, but it's not a property of the photons. You can only establish the correlation once you know how both detectors are angled, which means when you know the blue area. The phase vector of the photon never changed though, and was always going to result in that particular combination of measurements. That is, nothing spooky happened: we just increased our knowledge of the system.

 

[PeterDonis]

it's not a property of the photons

No, it's a property of the detectors. But it's a property of both detectors together, not of either one by itself. So it's not a local property since the detectors are spatially separated.

 

[Cthugha]

Right, but it's not a property of the photons. You can only establish the correlation once you know how both detectors are angled, which means when you know the blue area. The phase vector of the photon never changed though, and was always going to result in that particular combination of measurements. That is, nothing spooky happened: we just increased our knowledge of the system.

That is, however, still wrong. You need to establish the physical meaning of your "ellipse". What does it mean physically that the difference from the center to the outline of the ellipse changes? It cannot be the detection probability. If the detection probability can take any value that is not 0 or 1, you lose the perfect correlation or anticorrelation (unless you assume non-local influences or non-realism).

So what does your ellipticity mean physically for a real individual detector? What is the physical quantity it actually represents? If you cannot define the meaning of the ellipse without involving the second detector, it is a non-local property.

 

[Leureka]

No, it's a property of the detectors. But it's a property of both detectors together, not of either one by itself. So it's not a local property since the detectors are spatially separated.

Sorry if I sound condescending or generally with a bad tone, but I want to point out now( before anyone thinks otherwise) that all my replies are made in good faith, with sincere effort to understand. I stress this because I know this subject is very touchy and prone to easy dismissal.

Having said that: yes it's a property of both detectors together so in that sense it is "non local", but there is nothing mysterious about the measurement itself, as was made a case for the photon correlations. There is no communication between detectors to agree on some angle to adopt, each is decided upon independently. The only interaction happens locally at the level of the photon with the phase of the detector: if the photon vector lies inside the correct semicircle, it will make the detector blip. Same for the other detector. Now we compare results, and see that, if the photon vector was inside BOTH semicircles, then both detectors will have blinked. We do this multiple times: since the photon vector is randomly oriented each time, with enough measurements we'll have swept the whole circle, and the number of coincident results will simply be the number of times that vector was lying inside both colored semicircles, which in turn is proportional to the overlap of the areas. Neither detector phases or photon vectors ever changed at the moment of measurement.

That is, however, still wrong. You need to establish the physical meaning of your "ellipse". What does it mean physically that the difference from the center to the outline of the ellipse changes? It cannot be the detection probability. If the detection probability can take any value that is not 0 or 1, you lose the perfect correlation or anticorrelation (unless you assume non-local influences or non-realism).

So what does your ellipticity mean physically for a real individual detector? What is the physical quantity it actually represents? If you cannot define the meaning of the ellipse without involving the second detector, it is a non-local property.

I hope I understood your point: no the probability does not change, the photon vector can be imagined as simply a direction with no inherent lenght, so it will always sweep the full lenght of the radius.

As far as the meaning of the geometry, I'm afraid I haven't got around to it yet. Was hoping to spark some discussion here in that sense. I just wanted to show that in principle, there is a way to define the measurement correlations locally. It's not very different from the current understanding of the phenomenon: how can a non-local interaction happen? As far as i know, nobody knows; we don't even understand why photons obey a cos^2(x) probability. This does not mean there can't be a physical quantity associated with the ellipse (which wouldn't actually be an ellipse, but a different form that overlaps with a cosine dependence) until proven otherwise.

 

[PeterDonis]

yes it's a property of both detectors together so in that sense it is "non local"

Which means it violates the assumptions of Bell's theorem. So yes, a "non local" model in this sense can produce violations of the Bell inequalities.

 

[Leureka]

Which means it violates the assumptions of Bell's theorem. So yes, a "non local" model in this sense can produce violations of the Bell inequalities.

Isn't the whole point of the theorem that local variables can't influence the outcome of measurements? In my model, each measurement is determined locally. It's just the correlations that are, in a sense, non-local, but only because you need multiple measurements to get those correlations in the first place.

 

[PeterDonis]

Isn't the whole point of the theorem that local variables can't influence the outcome of measurements?

No.

In my model, each measurement is determined locally.

That is equally true of the quantum mechanical model: each measurement result is determined locally, by the interaction of the photon and the detector.

It's just the correlations that are, in a sense, non-local

Yes, that's the case for the QM model.

but only because you need multiple measurements to get those correlations in the first place

Yes, that's the case for the QM model.

I would strongly recommend reading Bell's actual papers so you can see what the actual assumptions behind Bell's theorem are. Many second-hand treatments do not do a good job of making that clear.

 

[Leureka]

No.That is equally true of the quantum mechanical model: each measurement result is determined locally, by the interaction of the photon and the detector.Yes, that's the case for the QM model.Yes, that's the case for the QM model.

I would strongly recommend reading Bell's actual papers so you can see what the actual assumptions behind Bell's theorem are. Many second-hand treatments do not do a good job of making that clear.

Alright. If that's the case I don't understand all the fuss about the theorem then. I tried reading the paper but I found it hard to follow, that's why I always tried to look for visualizations.

 

[Nugatory]

There is no communication between detectors to agree on some angle to adopt, each is decided upon independently. The only interaction happens locally at the level of the photon with the phase of the detector: if the photon vector lies inside the correct semicircle, it will make the detector blip. Same for the other detector. Now we compare results, and see that, if the photon vector was inside BOTH semicircles, then both detectors will have blinked. We do this multiple times: since the photon vector is randomly oriented each time, with enough measurements we'll have swept the whole circle, and the number of coincident results will simply be the number of times that vector was lying inside both colored semicircles, which in turn is proportional to the overlap of the areas. Neither detector phases or photon vectors ever changed at the moment of measurement.

You have demonstrated that at pair creation time you can assign a hidden variable to the photons in a way that produces the correct correlations when we have two detectors arranged at any angle relative to one another (at least in the case of a circular region - I'd have to see a worked example of the elliptical case to be sure of that part). That's not a surprising result, it's just Malus's Law for linearly polarized light with the polarization vector as the "hidden" variable (and arguments along those lines are why it took more than three decades for anyone to notice the incompatibility between the QM prediction and local hidden variable theories).

Look at @DrClaude 's #11 above. To violate Bell's inequality you will have to assign your hidden variable in such a way that when we consider three detector angles, one choice of the hidden variable will produce the predicted correlation for all nine possible combinations of detector angles.

 

[PeterDonis]

I tried reading the paper but I found it hard to follow

The key condition for this discussion is the factorizability condition. If we label the detector settings as A and B, and the "hidden variables" (in your setup that would be the direction of the "photon vector") as $\lambda$, then "locality" by Bell's definition means that the probability of a match (in your setup, a blip on both detectors) must factorize into a function of A and $\lambda$ only, and a function of B and $\lambda$ only. Whereas the most general form of the probability of a match would be a function of A, B, and $\lambda$.

The QM probability does not factorize as described above, so it can violate the Bell inequalities.

Your description of your setup doesn't include any math, so we have no way to know whether the probability of a match will factorize as described above unless you construct a mathematical model of your setup. If you did that, there would be two possibilities:

(1) The probability does factorize for your setup; that means your assumption that you can reproduce the QM probabilities (which violate the Bell inequalities) with your setup must be wrong. (The obvious place to look for where it goes wrong would be your assumption that you can find a shape that reproduces the $\cos^2$ probability function of QM.)

(2) The probability does not factorize for your setup. (This was what I assumed to be the case in my post #20.) In this case your setup can of course produce probabilities that violate the Bell inequalities, because it violates the assumptions of Bell's theorem.

 

[DrChinese]

1. It is my understanding that each time a photon arrives at one of the detectors, there is fundamentally a 50/50 chance the detector will blip or not. It is only when I combine my results with those from the other detector that i will see there actually is a correlation between the results, and this will depend on the angle between the detectors, which on a surface level seems spooky because how can each photon know what the other photon did, as to preserve the correlations?

2. For example, for angles at 22.5 degrees there is an overall 85% correlation. Which means, in a set of 10 measurements, around 8 of them will be the same, even though at each detector the total distribution is 50%...
View attachment 325977
3. But here's an explanation which involves entirely local variables that can come up with the exact same distribution.
Imagine a vector in a circle. With respect to the horizontal, this vector can take on any angle from 0 to 360 degrees. This can represent some kind of hidden phase the two entangled photons have in common (in the image below, one is colored yellow and another is red; these are just different independent vectors, as if they were on different pairs of photons).

4. Now what happens at the moment of measurement? There is an angle choice, but no matter what this angle choice is, there will always be a 50% chance to measure the photon. I represented this by coloring half the circle in blue. If the phase vector lands inside the blue area, the detector will blip. What the angle choice does, is rotate the circle. The phase vector is invariant, but it has a definite inclination with the respect to the measurement angle, which is simply the horizontal cutting the circle in two.

4. In essence, the correlations are an interplay between the state of the photons and the state of the detector.

Comments anyone? Where did i go wrong? Are my assumptions incorrect for example? Did I misunderstand experimental results?

Yes, you have misunderstood a few things. Perhaps I can provide a few specifics.

1. Most serious Bell tests use a polarizing beam splitter (PBS) or similar (such as a Wollaston prism). These have a detection probability near 100%. Instead of recording a hit or a miss, they record H for Horizontal or V for Vertical (or T for transmit and R for reflect). When there is agreement for the 2 photons, it is because the results are HH or VV. When there is disagreement, the results are HV or VH.

https://arxiv.org/pdf/quant-ph/9810080.pdf

In your presentation of checks and Xs, you have 4 cases in which there are 2 Xs. If neither of the photons are detected, how could you know they ever even existed? Entangled photon pairs occur at random times. If you don't detect anything for either of the pair, you won't be able to record that case at all. Hence why Bell tests use a PBS with a detector at each output port. They need 4 detectors total: 2 for each PBS (one PBS on left side, one PBS on right side).2. Your statistics (85% match) are correct for the 22.5 degree case. Note this is what actually occurs, and is not necessarily what your model will yield.3. Here is where your problems arise, and there are several of them.

a. Your local hidden variables are the red and yellow "phase" vectors. You say the photons have these "in common". On the other hand, you describe them "as if they are on different pairs of photons". My assumption is that you are in essence trying to show that the red is what we might call trial 1, and the yellow is trial 2. If this assumption is incorrect, please let me know. For each trial, we have photons L (Left circle) and R (Right circle) which are entangled and encounter a detector which is model by the blue semi-circle. If this is incorrect, please let me know.

b. The 4 different detector cases are not drawn to scale and are off by a factor of 2. Your 90 degree case (the 4th) is drawn as if they are 180 degrees apart - even though your purported statistics match what would actually occur in experiments with a PBS.

c. So... you will need to be explicit about your formula, because from the drawing it is not clear when we will get an H outcome on one side, or when we will get a V instead. I would expect your rule(s) to spell out how you get those. Note that the @PeterDonis comment about each rule applying separately is critical. The results must occur independently if you are pushing a local model.

As I understand your rule: if there is overlap with the semi-circle and the colored line, then the outcome is certain for that side (either L or R). This does in fact "work" for the 0 degree, 90 degree, and probably the 45 degree cases. But...

d. Here is where your model goes wrong. You claim - without providing a formula to match - that the 22.5 degree case yields the correct 85% results. It doesn't!! Your model actually yields a 75% match rate, well off from the true expectation value. That's because the overlap between the 2 semi-circles (L and R) is only 75%. It's that overlap % that drives your formula. (i.e. That's how it works for the other 3 cases - 0%, 50%, 100%.) A more rigorous mathematical derivation of this result is possible, but suffice it to say that you cannot "fix" the 22.5 degree case without breaking one of the other cases. 4. Additional comments:

a. As I mention, the true quantum prediction does not include a term for the individual angle settings - only the difference. Adding a single common hidden variable for both the L and R outcomes can never - no matter how complex you make it - can never suffice. Adding even more hidden variables does nothing either.

b. The Bell paper @PeterDonis references actually refutes a variation of your model (the spin 1/2 version) before proceeding to prove why no hidden variable model can be constructed to match the quantum statistics.

https://www.informationphilosopher.com/solutions/scientists/bell/Bell_On_EPR.pdf

c. Finally: it was discovered post-Bell that entangled pairs of photons do NOT need to even to have a common initial source. Pairs of photons are now routinely created that have never existed in a common region of space time. Pretty hard to have your common "phase vector" when they don't have any aspect of their existence (creation or detection or anywhere in between) in common. (Assuming locality, of course.)

https://arxiv.org/abs/0911.1314

 

[WernerQH]

I tried reading the paper but I found it hard to follow, that's why I always tried to look for visualizations.

Years ago David Mermin wrote an article Bringing home the atomic world: Quantum mysteries for anybody. Perhaps you find that easier to read. (It's about an analogous experiment with spin-$\frac 1 2$ particles; for photons the angular distribution is different.)

Your algorithm doesn't sound very complicated. You could write a small computer program to simulate the Aspect et al experiment. Analyzing the behaviour of your program you should be able to find out why it doesn't produce the quantum mechanical predictions.

 

[Leureka]

Yes, you have misunderstood a few things. Perhaps I can provide a few specifics.

1. Most serious Bell tests use a polarizing beam splitter (PBS) or similar (such as a Wollaston prism). These have a detection probability near 100%. Instead of recording a hit or a miss, they record H for Horizontal or V for Vertical (or T for transmit and R for reflect). When there is agreement for the 2 photons, it is because the results are HH or VV. When there is disagreement, the results are HV or VH.

https://arxiv.org/pdf/quant-ph/9810080.pdf

In your presentation of checks and Xs, you have 4 cases in which there are 2 Xs. If neither of the photons are detected, how could you know they ever even existed? Entangled photon pairs occur at random times. If you don't detect anything for either of the pair, you won't be able to record that case at all. Hence why Bell tests use a PBS with a detector at each output port. They need 4 detectors total: 2 for each PBS (one PBS on left side, one PBS on right side).2. Your statistics (85% match) are correct for the 22.5 degree case. Note this is what actually occurs, and is not necessarily what your model will yield.3. Here is where your problems arise, and there are several of them.
View attachment 325994
a. Your local hidden variables are the red and yellow "phase" vectors. You say the photons have these "in common". On the other hand, you describe them "as if they are on different pairs of photons". My assumption is that you are in essence trying to show that the red is what we might call trial 1, and the yellow is trial 2. If this assumption is incorrect, please let me know. For each trial, we have photons L (Left circle) and R (Right circle) which are entangled and encounter a detector which is model by the blue semi-circle. If this is incorrect, please let me know.

b. The 4 different detector cases are not drawn to scale and are off by a factor of 2. Your 90 degree case (the 4th) is drawn as if they are 180 degrees apart - even though your purported statistics match what would actually occur in experiments with a PBS.

c. So... you will need to be explicit about your formula, because from the drawing it is not clear when we will get an H outcome on one side, or when we will get a V instead. I would expect your rule(s) to spell out how you get those. Note that the @PeterDonis comment about each rule applying separately is critical. The results must occur independently if you are pushing a local model.

As I understand your rule: if there is overlap with the semi-circle and the colored line, then the outcome is certain for that side (either L or R). This does in fact "work" for the 0 degree, 90 degree, and probably the 45 degree cases. But...

d. Here is where your model goes wrong. You claim - without providing a formula to match - that the 22.5 degree case yields the correct 85% results. It doesn't!! Your model actually yields a 75% match rate, well off from the true expectation value. That's because the overlap between the 2 semi-circles (L and R) is only 75%. It's that overlap % that drives your formula. (i.e. That's how it works for the other 3 cases - 0%, 50%, 100%.) A more rigorous mathematical derivation of this result is possible, but suffice it to say that you cannot "fix" the 22.5 degree case without breaking one of the other cases.4. Additional comments:

a. As I mention, the true quantum prediction does not include a term for the individual angle settings - only the difference. Adding a single common hidden variable for both the L and R outcomes can never - no matter how complex you make it - can never suffice. Adding even more hidden variables does nothing either.

b. The Bell paper @PeterDonis references actually refutes a variation of your model (the spin 1/2 version) before proceeding to prove why no hidden variable model can be constructed to match the quantum statistics.

https://www.informationphilosopher.com/solutions/scientists/bell/Bell_On_EPR.pdf

c. Finally: it was discovered post-Bell that entangled pairs of photons do NOT need to even to have a common initial source. Pairs of photons are now routinely created that have never existed in a common region of space time. Pretty hard to have your common "phase vector" when they don't have any aspect of their existence (creation or detection or anywhere in between) in common. (Assuming locality, of course.)

https://arxiv.org/abs/0911.1314

1) i did not know this. I thought entangled photon pairs were created on demand. I'm not exactly sure how this affects my idea though, since you can freely change what the blue area stands for.
3a) correct.
3b) yes I'm aware they're off a factor of two, but it is just for ease of presentation. This way you can clearly see the area overlap is 50%, 0%... If I wanted to keep the right angles i would have used two semicircles (half white half blue) instead, and rotate them a maximum of 90°, but I thought this was a better visualization. Admittedly it's not the best drawing but I can't fix it right now.
3c) the rule is if the vector falls into the colored area, the detector blips. A photon vector is just some undetermined property of the photon that is constant from it's departure from the source (not necessarily polarization, i just haven't thought about it), and is the same for both entangled partners.
3d) this is an issue with the circle representation, because the area overlap scales linearly with the angle rotation, which obviously means that what you said is true. Further below I've shown that you can get non-linear overlaps with angles, if your shape is not an exact circle. I haven't figured out the exact shape that would reproduce a cos^2 dependence, which is a valid objection and another reason why I posted this, but I don't think is impossible.
4c) Aren't those photons still entangled though? Regardless of the origin of the entanglement, the vector being the same would be a requisite for them to be entangled. Whatever the process that created the entanglement, also "aligned" the vectors. As I said, the vector i presented does not necessarily represent polarization.
Overall, I liked how PeterDonis put it. I still have to fully comprehend what it means to have factorizable probabilities in this context, but I'll dig deeper into it. I also agree that one way to show this wrong is to somehow prove that no overlapping, rotating shapes can reproduce a cosine dependence.@WernerQH thanks, I'll definitely take a look. It's harder than it looks I'm afraid, because first i need to find an algorithm that can find a shape to scale the overlapping area correctly, with a cosine^2 dependence.

 

[PeroK]

@WernerQH thanks, I'll definitely take a look. It's harder than it looks I'm afraid, because first i need to find an algorithm that can find a shape to scale the overlapping area correctly, with a cosine^2 dependence.

It may be worth highlighting that the Bell inequality itself is quite simple. If we assume that the detectors are independent of the particles, then however the hidden variables are constructed, they must be distributed according to:
$$N_1: (+, +, +) \ \ \ (-,-,-)$$$$N_2: (+, +, -) \ \ \ (-,-,+)$$$$N_3: (+, -, +) \ \ \ (-,+,-)$$$$N_4: (+, -, -) \ \ \ (-,+,+)$$$$N_5: (-, +, +) \ \ \ (+,-,-)$$$$N_6: (-, +, -) \ \ \ (+,-,+)$$$$N_7: (-, -, +) \ \ \ (+,+,-)$$$$N_8: (-, -, -) \ \ \ (+,+,+)$$Where $N_i$ is the number/probability of that configuration of hidden variables with respect to any three angles of the two particles. If you don't have that, then you're not talking about the basic scenario of two entangled particles. Having three different angles is the mimimum in order to generate a distinction between classical and QM predictions.

Then, it's a relatively simple matter to show that you cannot find any distribution of $N_1$ to $N_8$ to reproduce the QM statistics for certain combinations of angles. Note that the QM calculation uses complex probability amplitudes, rather than classical probabilities. And, thereby, can achieve higher levels of correlation that are impossible for classical probabilities.

Then the Bell test is to show that nature produces correlations beyond the classical limit. And, not only that, but in complete agreement with the predictions of QM.

The argument against QM then becomes somewhat wilfully contrary, IMHO.

 

[Leureka]

It may be worth highlighting that the Bell inequality itself is quite simple. If we assume that the detectors are independent of the particles, then however the hidden variables are constructed, they must be distributed according to:
$$N_1: (+, +, +) \ \ \ (-,-,-)$$$$N_2: (+, +, -) \ \ \ (-,-,+)$$$$N_3: (+, -, +) \ \ \ (-,+,-)$$$$N_4: (+, -, -) \ \ \ (-,+,+)$$$$N_5: (-, +, +) \ \ \ (+,-,-)$$$$N_6: (-, +, -) \ \ \ (+,-,+)$$$$N_7: (-, -, +) \ \ \ (+,+,-)$$$$N_8: (-, -, -) \ \ \ (+,+,+)$$Where $N_i$ is the number/probability of that configuration of hidden variables with respect to any three angles of the two particles. If you don't have that, then you're not talking about the basic scenario of two entangled particles. Having three different angles is the mimimum in order to generate a distinction between classical and QM predictions.

Then, it's a relatively simple matter to show that you cannot find any distribution of $N_1$ to $N_8$ to reproduce the QM statistics for certain combinations of angles. Note that the QM calculation uses complex probability amplitudes, rather than classical probabilities. And, thereby, can achieve higher levels of correlation that are impossible for classical probabilities.

Then the Bell test is to show that nature produces correlations beyond the classical limit. And, not only that, but in complete agreement with the predictions of QM.

The argument against QM then becomes somewhat wilfully contrary, IMHO.

I'm not really arguing one way or another, and i'm definitely not willfully contrary. I'm basing all this on popular explanations i found online, and basically all of them used explanations with two angles. I'm curious though, how do you create three angle correlations with pairs of polarized photons?

 

[Nugatory]

I'm curious though, how do you create three angle correlations with pairs of polarized photons?

We position the detectors in different configurations while we run a large number of entangled pairs through our experiment. Eventually we end up with statistically significant results for the AB correlation, the BC correlation, and the AC correlation.

You may think you see a flaw in this approach: if particles with a particular value of the hypothetical hidden variable are hypothetically more likely to be detected in one of the three configurations than the other two the correlations will be not be calculated from equivalent subsets of the pairs. This is the well-known “fair sampling loophole”, and more sophisticated experiments have been able to close it.

 

[DrChinese]

1) i did not know this. I thought entangled photon pairs were created on demand. I'm not exactly sure how this affects my idea though, since you can freely change what the blue area stands for.

3c) the rule is if the vector falls into the colored area, the detector blips. A photon vector is just some undetermined property of the photon that is constant from it's departure from the source (not necessarily polarization, i just haven't thought about it), and is the same for both entangled partners.

3d) this is an issue with the circle representation, because the area overlap scales linearly with the angle rotation, which obviously means that what you said is true. Further below I've shown that you can get non-linear overlaps with angles, if your shape is not an exact circle. I haven't figured out the exact shape that would reproduce a cos^2 dependence, which is a valid objection and another reason why I posted this, but I don't think is impossible.

... Overall, I liked how PeterDonis put it. I still have to fully comprehend what it means to have factorizable probabilities in this context, but I'll dig deeper into it. ... i need to find an algorithm that can find a shape to scale the overlapping area correctly, with a cosine^2 dependence.

4c) Aren't those photons still entangled though? Regardless of the origin of the entanglement, the vector being the same would be a requisite for them to be entangled. Whatever the process that created the entanglement, also "aligned" the vectors.

1) Your model can be adjusted for this, yes. Just wanted to make sure you understood how PDC works. The ratio of photons that enter the crystal to the number that are converted to entangled pairs is on the order of 100 million to 1. It's completely random.

3c and 3d) That's what I thought. Yours is the one of the most common initial models to consider. But unfortunately it cannot be "fixed" to present the quantum expectation value (cos^2). A tweak to the model to make it appear to work at one angle simply breaks the model elsewhere.

Please be aware that for a number of years, it was assumed that a model might be developed that would work (as you have attempted). Of course, that was before Bell's 1964 paper proved conclusively that no such model was possible. Once you add in the Bell's requirement that there can be no coordination or communication between the L and the R detector settings for the separate outcomes - a requirement sometimes referred to as "realism" or "non-contextuality" - then everything falls apart.

4c) These photons are entangled after they are created, and never have interacted. The act of entangling them is done remotely (i.e. at a distance in spacetime) in a process called entanglement swapping (which is a form of quantum teleportation). They can't have the same initial phase vector, even accidently or coincidentally. Of course, the details of such swapping is pretty complex and there is no point of analyzing how swapping works until you understand why Bell prevents the development of a local realistic model of entanglement.

The existence of even one experiment demonstrating entanglement of photons that have never existed in a common region of spacetime should be enough to exclude all local realistic models of entanglement. It's not even clear a nonlocal realistic model is feasible at this point.

 

[PeroK]

I'm basing all this on popular explanations i found online, and basically all of them used explanations with two angles.

Bell's inequality uses three angles. See, for example, Modern QM by JJ Sakurai. By using three different angles, it becomes impossible for classical probabilities to achieve the experimental results.

I think I understand what you are doing now. By using two angles, you are trying to show that hidden variables can reproduce the $\cos^2$ distribution. I can see how that might also be impossible, but it's not the basis of Bell's inequality and Theorem.

I'm curious though, how do you create three angle correlations with pairs of polarized photons?

You have two detectors that can each be set at three different angles.

 

[PeroK]

I'm curious though, how do you create three angle correlations with pairs of polarized photons?

Here's is Bell's inequality. We intend to measure spin or polarization at each of the two detectors for (the same) three different angles. First, we have the distibution of hidden variables that I posted above. Whatever the overall distribution of variables, it must boil down to some distibution for any three given angles. I'll write these as probabilities this time:
$$p_1: (+, +, +) \ \ \ (-,-,-)$$$$p_2: (+, +, -) \ \ \ (-,-,+)$$$$p_3: (+, -, +) \ \ \ (-,+,-)$$$$p_4: (+, -, -) \ \ \ (-,+,+)$$$$p_5: (-, +, +) \ \ \ (+,-,-)$$$$p_6: (-, +, -) \ \ \ (+,-,+)$$$$p_7: (-, -, +) \ \ \ (+,+,-)$$$$p_8: (-, -, -) \ \ \ (+,+,+)$$Let's label the angles as $a, b, c$ in the order given. We now do a large number of experiments and vary the detectors, so that we have a large number of experiments where the two detectors are set at different angles: detector 1 at angle $a$ with dector 2 at angle $b$; detector 1 at angle $a$ with detector 2 at angle $c$; detector 1 at angle $b$, with detector 2 at angle $c$; and, vice versa. We now look at some cases:
$$p(a+, b+) = p_3+p_4$$This is the case where we have the first detector set to angle $a$ and get $+$ and also have the second detector set to angle $b$ and get $+$ as well.

Now, this is Bell's idea using the third angle, we also have
$$p(a+, c+) = p_2 + p_4$$$$p(c+, b+) = p_3 + p_7$$This gives us the inequality:
$$p(a+, b+) \le p(a+,c+) + p(c+, b+)$$This is because the left-hand side is just $p_3 + p_4$ and the right-hand side is $p_3 + p_4 + p_2 + p_7$.

The final thing is to show that QM predicts a violation of this inequality in some cases. We can let $a = 0, b= 2\theta$ and $c = \theta$. So, the third angle bisects the other two. Now, QM predicts:
$$p(a+, b+) = \sin^2 \theta $$$$p(a+, c+) = p(c+, b+) = \sin^2 \frac \theta 2$$And, Bell's inequality only holds if we have:
$$\sin^2 \theta \le 2\sin^2 \frac \theta 2$$You can actually see now where the issue of non-linearity of the $\sin^2$ distribution is critical. Although, note that it took the introduction of a third, intermediate angle to force the contradiction.

In any case, this equaility simply does not hold. In fact, if we use the trig identities $2\sin^2 \frac \theta 2 = 1 - \cos \theta$ and $\sin^2 \theta = 1 - \cos^2 \theta$, then Bell's inequality becomes:
$$\cos \theta < cos^2 \theta$$Which fails for any angle $0 < \theta < \frac \pi 2$.

This mathematics proves that your supposed elliptical distribution (or any distribution) cannot reproduce the QM probability distribution in all cases. All classical distributions must obey Bell's inequality - which QM violates.

In any case, that is Bell's inequality and why QM violates it.

 

[Leureka]

Here's is Bell's inequality. We intend to measure spin or polarization at each of the two detectors for (the same) three different angles. First, we have the distibution of hidden variables that I posted above. Whatever the overall distribution of variables, it must boil down to some distibution for any three given angles. I'll write these as probabilities this time:
$$p_1: (+, +, +) \ \ \ (-,-,-)$$$$p_2: (+, +, -) \ \ \ (-,-,+)$$$$p_3: (+, -, +) \ \ \ (-,+,-)$$$$p_4: (+, -, -) \ \ \ (-,+,+)$$$$p_5: (-, +, +) \ \ \ (+,-,-)$$$$p_6: (-, +, -) \ \ \ (+,-,+)$$$$p_7: (-, -, +) \ \ \ (+,+,-)$$$$p_8: (-, -, -) \ \ \ (+,+,+)$$Let's label the angles as $a, b, c$ in the order given. We now do a large number of experiments and vary the detectors, so that we have a large number of experiments where the two detectors are set at different angles: detector 1 at angle $a$ with dector 2 at angle $b$; detector 1 at angle $a$ with detector 2 at angle $c$; detector 1 at angle $b$, with detector 2 at angle $c$; and, vice versa. We now look at some cases:
$$p(a+, b+) = p_3+p_4$$This is the case where we have the first detector set to angle $a$ and get $+$ and also have the second detector set to angle $b$ and get $+$ as well.

Now, this is Bell's idea using the third angle, we also have
$$p(a+, c+) = p_2 + p_4$$$$p(c+, b+) = p_3 + p_7$$This gives us the inequality:
$$p(a+, b+) \le p(a+,c+) + p(c+, b+)$$This is because the left-hand side is just $p_3 + p_4$ and the right-hand side is $p_3 + p_4 + p_2 + p_7$.

The final thing is to show that QM predicts a violation of this inequality in some cases. We can let $a = 0, b= 2\theta$ and $c = \theta$. So, the third angle bisects the other two. Now, QM predicts:
$$p(a+, b+) = \sin^2 \theta $$$$p(a+, c+) = p(c+, b+) = \sin^2 \frac \theta 2$$And, Bell's inequality only holds if we have:
$$\sin^2 \theta \le 2\sin^2 \frac \theta 2$$You can actually see now where the issue of non-linearity of the $\sin^2$ distribution is critical. Although, note that it took the introduction of a third, intermediate angle to force the contradiction.

In any case, this equaility simply does not hold. In fact, if we use the trig identities $2\sin^2 \frac \theta 2 = 1 - \cos \theta$ and $\sin^2 \theta = 1 - \cos^2 \theta$, then Bell's inequality becomes:
$$\cos \theta < cos^2 \theta$$Which fails for any angle $0 < \theta < \frac \pi 2$.

This mathematics proves that your supposed elliptical distribution (or any distribution) cannot reproduce the QM probability distribution in all cases. All classical distributions must obey Bell's inequality - which QM violates.

In any case, that is Bell's inequality and why QM violates it.

One thing that is still not clear to me: why do you group up the different measurements? (In the following D1 stands for detector 1 and D2 for detector2, while a b c are the angles)

We measure D1A and D2B, we get a probability distribution P1 (for example, getting both +);
Similarly we do D1A and D2C, getting P2.
Finally, we do D1C and D2B, getting P3.

Let's say, for example, a=0°, b=22.5°, c=45°.
We get something like this:

P1(A/B) (+ +, + -, - +, - -) = P(22.5°) (42.5%, 15%, 15%, 42.5%)

P2(A/C) (+ +, + -, - +, - -) = P(45°) (25%, 25%, 25%, 25%)

P3(B/C) (+ +, + -, - +, - -) = P(22.5°) (42.5%, 15%, 15%, 42.5%)(It looks to me like D1A/D2B should give the exact same distribution as D1B/D2A, since the detectors are identical. The same applies to P2 and P3.)

In the end, you group up all the cases: like for all the times where D1A got +, you count how many got D2B+ and D2C+. But how can you assign a probability distribution to these combinations? P1 (D1A+/D2B+) is independent from P2 (D1A+/D2C+) or P3. I don't understand how you can assign some P to (+ - -) (- + + ). It's clear you can't just add the probabilities up: for (+ - -) (- + + ), it would be 42.5% (D1A+, D2B+) + 25% (D1A+, D2C+) + 15% (D1C-, D2B+) which is 82.5% (makes no sense for only one distribution).

It's possible Im missing some probability calculus rule here, it's not my forte.