- #1
charmed1j
- 3
- 0
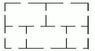
Homework puzzle from 15 years ago never solved - Please Help!
 I had this puzzle in one of my math classes in Jr. High - for 15 years I have been trying to solve it - no one would ever give me the answer, and I was sick on the day the teacher gave it. He has since retired, and no one from my class remembers how to do it. Please help! LOL
I had this puzzle in one of my math classes in Jr. High - for 15 years I have been trying to solve it - no one would ever give me the answer, and I was sick on the day the teacher gave it. He has since retired, and no one from my class remembers how to do it. Please help! LOL
I am tired of killing trees by wasting paper on it.
Jennifer Vogt
charmed1@chartermi.net
I am tired of killing trees by wasting paper on it.
Jennifer Vogt
charmed1@chartermi.net