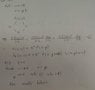- #1
Homogeneous function of degree n
- Thread starter athrun200
- Start date
-
- Tags
- Degree Function Homogeneous
In summary, a homogeneous function of degree n is a mathematical function where all variables involved are raised to the power of n. It can be determined if a function is homogeneous by substituting all variables with a constant raised to the power of n and seeing if the result is equal to the original function multiplied by that constant raised to the power of n. Homogeneous functions have practical applications in various fields and have unique properties that make them useful in certain situations. A function can only be homogeneous of one degree, and graphing a homogeneous function of degree n can be done using a computer or manually plotting points to create a symmetrical graph known as a homothetic curve.
FAQ: Homogeneous function of degree n
What is a homogeneous function of degree n?
A homogeneous function of degree n is a mathematical function where all variables involved are raised to the power of n. This means that if you were to multiply all of the variables by a constant, the result would be the same as if you had multiplied the original function by that constant raised to the power of n.
How can I determine if a function is homogeneous or not?
To determine if a function is homogeneous, you can perform a simple test by substituting all variables with a constant raised to the power of n. If the result is equal to the original function multiplied by that constant raised to the power of n, then the function is homogeneous.
What is the significance of homogeneous functions in mathematics?
Homogeneous functions have many practical applications in mathematics, including optimization problems, economics, and physics. They also have unique properties that make them easier to work with in certain situations, such as when using the Euler's Homogeneous Function Theorem.
Can a function be homogeneous of more than one degree?
No, a function can only be homogeneous of one degree. This is because a function can only have one set of variables that are raised to the same power. If a function has multiple sets of variables with different powers, it is not considered homogeneous.
How do I graph a homogeneous function of degree n?
Graphing a homogeneous function of degree n can be done by using a computer or graphing calculator. You can also manually plot points by choosing values for the variables and calculating the corresponding output. The resulting graph will have a symmetrical shape, known as a homothetic curve.