- #1
roam
- 1,271
- 12
I am trying to estimate the second derivative of ##sin(x)## at ##0.4## for ##h=10^{-k}, \ \ k=1, 2, ..., 20## using:
$$\frac{f(x+h)-2f(x)+f(x-h)}{h^2}, \ \ (1)$$
I know the exact value has to be ##f''(0.4)=-sin(0.4)= -0.389418342308651.##
I also want to plot the error as a function ##h## in Matlab.
According to my textbook equation (1) has error give by ##h^2f^{(4)}/12##. So I am guessing ##f^{(4)}## refers to the fifth term in the Taylor expansion which we can find using Matlab syntax taylor(f,0.4):
sin(2/5) - (sin(2/5)*(x - 2/5)^2)/2 + (sin(2/5)*(x - 2/5)^4)/24 + cos(2/5)*(x - 2/5) - (cos(2/5)*(x - 2/5)^3)/6 + (cos(2/5)*(x - 2/5)^5)/120
So substituting this in, here is my code for ##f''(0.4)## and error so far:
But this does not converge and I get some strange values for ##f''## which are very different from the exact value I found above:
What is wrong with my code?
And for the error I get all zeros, so it is not possible to plot error vs h. But I believe the graph should look something like this image:
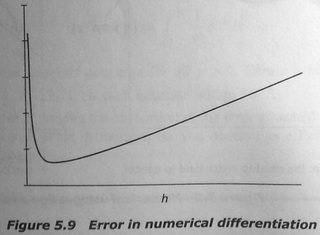
So, what do I need to do here?
Any help would be greatly appreciated.
$$\frac{f(x+h)-2f(x)+f(x-h)}{h^2}, \ \ (1)$$
I know the exact value has to be ##f''(0.4)=-sin(0.4)= -0.389418342308651.##
I also want to plot the error as a function ##h## in Matlab.
According to my textbook equation (1) has error give by ##h^2f^{(4)}/12##. So I am guessing ##f^{(4)}## refers to the fifth term in the Taylor expansion which we can find using Matlab syntax taylor(f,0.4):
sin(2/5) - (sin(2/5)*(x - 2/5)^2)/2 + (sin(2/5)*(x - 2/5)^4)/24 + cos(2/5)*(x - 2/5) - (cos(2/5)*(x - 2/5)^3)/6 + (cos(2/5)*(x - 2/5)^5)/120
So substituting this in, here is my code for ##f''(0.4)## and error so far:
Code:
format long
x=0.4;
for k = 1:1:20
h=10.^(-k);
ddf=(sin(x+h)-2*sin(x)+sin(x-h))./(h.^2)
e=((h.^2)*((cos(2/5)*(x - 2/5).^3)/6))./12
plot(h,e)
endBut this does not converge and I get some strange values for ##f''## which are very different from the exact value I found above:
Code:
ddf = -0.389093935175844
ddf = -0.389415097166723
ddf = -0.389418309876266
ddf = -0.389418342017223
ddf = -0.389418497448446
ddf = -0.389466237038505
ddf = -0.388578058618805
ddf = -0.555111512312578
ddf = 0.00
ddf = 0.00
ddf = -5.551115123125782e+05
ddf = 0.00
ddf = 0.00
ddf = 0.00
ddf = -5.551115123125782e+13
ddf = 0.00
ddf = 0.00
ddf = 0.00
ddf = 0.00
ddf = 0.00What is wrong with my code?
And for the error I get all zeros, so it is not possible to plot error vs h. But I believe the graph should look something like this image:
So, what do I need to do here?
Any help would be greatly appreciated.