How addition of vectors works if every force is quantized

[danielhaish]

Assuming two forces applied on an object in two vector one horizontal to the object and the other vertical,
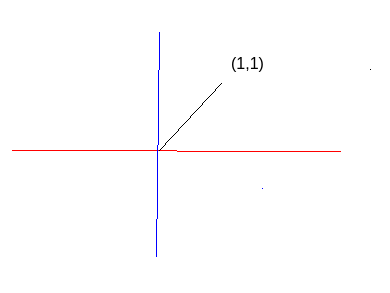
By vector addition the resulting vector would be in 45 degrees.
(0,1) + (1,0) = (1,1)
So the object acceleration direction would be as the following graph.

But if the force that hinting the object is quantized and the effect of the particle hitting the object is immediate, Then in low speeds the object will first accelerate in one direction and then accelerate in the other direction which would change a bit the route of the object, Till it get to high speed and that effect would be not measurable like in the following graph

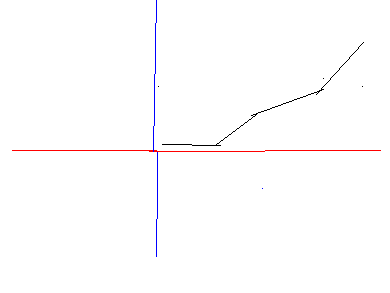
Is this difference in object route is measurable in low speeds?

 

[Nugatory]

But if the force that hinting the object is quantized….

That’s a big “if”.
When we’re thinking in terms of an object changing position in response to an applied force, one way or another we are starting from Newton’s $F=ma$ in which $a$ is the second derivative of a continuous variable, $x$. Thus forces aren’t quantized the way you’re thinking so can always be added as vectors and the question never arises.

Is this difference in object route is measurable in low speeds?

The quantum mechanical calculation of expected positions of objects subject to forces uses a completely different mathematical framework, one in which there’s no notion of object route.

 

[anuttarasammyak]

If quantized you say is not different so much from probabilistic collision of particles around, Brownian motion might be of your interest.

 

[danielhaish]

That’s a big “if”.
When we’re thinking in terms of an object changing position in response to an applied force, one way or another we are starting from Newton’s $F=ma$ in which $a$ is the second derivative of a continuous variable, $x$. Thus forces aren’t quantized the way you’re thinking so can always be added as vectors and the question never arises.

The quantum mechanical calculation of expected positions of objects subject to forces uses a completely different mathematical framework, one in which there’s no notion of object route.

I don't see how I get this wrong, we may look at the specific case where there are two light beams places in 90 rotation, and they both moving 90 degrees to there front in the same speed so they are moving away from each other, And there is very light object between them in plate with friction so the object keep moving in at low speed that equal to 1/root 2 times
the speed of the light beams. Like in the following diagram

In case each photon would hit the object at difference time the path of the object would be longer, Then a case the object would be moving in 45 degrees. Are you saying that the path of the object would be very difference but some how balanced to the long run because of quantum mechanics equations. How this possible, Isn't moving in straight line will always be shorter then moving in some other path?

 

[Vanadium 50]

I don't see how I get this wrong,

QM does not have a quantum of force.

We can discuss what would happen in your drawing, but until we get past the main point,m we won't make progress.

 

[danielhaish]

QM does not have a quantum of force.

We can discuss what would happen in your drawing, but until we get past the main point,m we won't make progress.

I didnt say there is a quantum force I just said that every force have a particle that carry it so I talked about all forces in general. So basically my question is eather this effect I described could happend

 

[PeterDonis]

In case each photon would hit the object at difference time the path of the object

You are missing the point of post #2: if you are using a model in which you have "photons" hitting the object, then the object does not have a path in your model. You can't have it both ways. Either you use a classical model where the object has a path and the force is continuous, or you use a quantum model where you can talk about things like photons but the object does not have a path. You can't do both.

 

[danielhaish]

You are missing the point of post #2: if you are using a model in which you have "photons" hitting the object, then the object does not have a path in your model. You can't have it both ways. Either you use a classical model where the object has a path and the force is continuous, or you use a quantum model where you can talk about things like photons but the object does not have a path. You can't do both.

So by the qunatom model the changes in the object speed only accurs when hitted it by few photons? What happend after one phoon hit the object? Or one photon hitting the object would only change the chance of the object to have higher volcity

 

[PeroK]

I didnt say there is a quantum force I just said that every force have a particle that carry it so I talked about all forces in general. So basically my question is eather this effect I described could happend

There are a lot of threads on here where QM is assumed to be only a tweak to classical mechanics. Classical mechanics is assumed to remain valid, but QM is added, like adding a touch of tabasco sauce. This is no use as a starting point. QM is an entirely different description of nature that is highly non-classical. It's a completey different ball game.

 

[danielhaish]

There are a lot of threads on here where QM is assumed to be only a tweak to classical mechanics. Classical mechanics is assumed to remain valid, but QM is added, like adding a touch of tabasco sauce. This is no use as a starting point. QM is an entirely different description of nature that is highly non-classical. It's a completey different ball game.

Yes but my question is about waether the case of two forces apllied on a object would give diffrence amperic result then a case where only the resulting vector is applied on a object. Which is unexpected classicaly

 

[Dale]

if you are using a model in which you have "photons" hitting the object, then the object does not have a path in your model.

This!

 

[danielhaish]

This!

But what would give more accurate result to the finel position of the object

 

[PeterDonis]

So by the qunatom model the changes in the object speed only accurs when hitted it by few photons?

No, in the quantum model there is no "object speed", just as there is no "object path". Quantum is not classical. You are trying to think of it as a classical model. That doesn't work.

 

[PeterDonis]

But what would give more accurate result to the finel position of the object

"More accurate" compared to what? The whole point is that you don't have two models that are competing. Either you are in a regime where classical physics is a good enough approximation, in which case you use that, or you are in a regime where you need to use quantum physics, in which case you use that. Your scenario as you posed it in the OP is way too vague to even tell which regime it is in, since you have said nothing about what object you are using.

 

[Dale]

But what would give more accurate result to the finel position of the object

There is only one model where the object even has a definite final position. So the question presupposes the answer: the classical model.

 

[anuttarasammyak]

If quantized you say is not different so much from probabilistic collision of particles around, Brownian motion might be of your interest.

And in relaticistic QM, Zitterbewegung might give you some insight. By the theory particles keep trembling with light speed in region of compton wavelength.

 

[Vanadium 50]

I'm not a big fan of Zitterbewegung as a way to explain anything (but it is fun to say, like Farfignewton or whatever word VW used.)

I think the emerging consensus explanation, that this is a weird and unphysical mix of classical and quantum behavior is probably the best answer that is possible to give.

 

[berkeman]

(but it is fun to say, like Farfinewton or whatever word VW used.)

https://en.wiktionary.org/wiki/Fahrvergnügen

 

[Demystifier]

I see this thread as a question about addition of vectors in QM, not necessarily about force. So instead of force, let me consider the momentum. A particle in the 3-dimensional box has the momentum quantized in all 3 principal directions of the box. But the system is not rotational invariant (it's a box, not a sphere), so the momentum is not quantized in an arbitrary direction.

 

[PeterDonis]

Thread closed for moderation.

 

[PeterDonis]

After moderator review, the thread will remain closed as the OP question has been sufficiently addressed.