How Are Beam Support Reactions Calculated?

[Guillem_dlc]

Homework Statement

For the given loads, determine the reactions at the beam supports.

Relevant Equations

$\sum F=0, \sum M=0$

Figure:

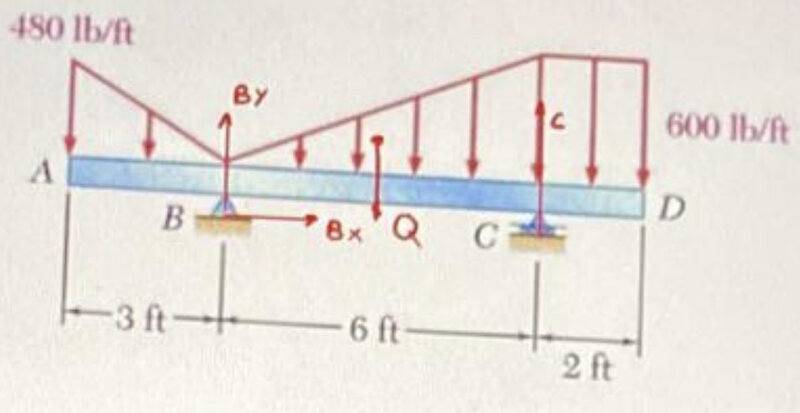
My attempt at a solution:

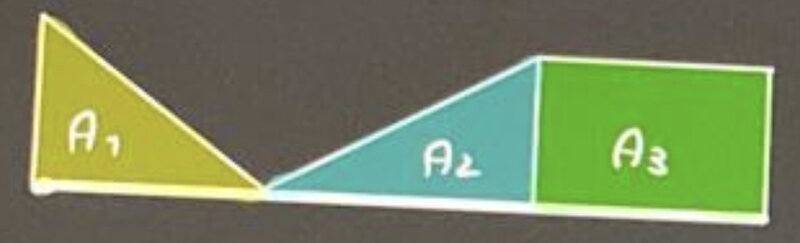
We know that $Q=A_T$
We calculate $Q$:
$$Q=\dfrac{3\cdot 480}{2}+\dfrac{600\cdot 6}{2}+600\cdot 2=3720\, \textrm{lb}$$
Then we look for the point $\overline{x}$ of the centre of gravity:
$$\overline{x_1}=1\, \textrm{ft},\quad \overline{x_2}=3+\dfrac63=5\, \textrm{ft},\quad \overline{x_3}=3+6+\dfrac22=10\, \textrm{ft}$$
$$\overline{x}=\dfrac{\sum x_iQ_i}{Q}=5,84\, \textrm{ft}$$
$$\sum Fx=\boxed{Bx=0}$$
$$\sum Fy=0=By+C-Q=0\rightarrow \boxed{By=1959,2\, \textrm{lb}}$$
$$\sum M_B=2,84Q-6C=0\rightarrow \boxed{C=1760,8\, \textrm{lb}}$$

Would this not be the case in this one? It's just that the solution tells me the following and I don't get that centre of gravity in area 2:
Official solution:

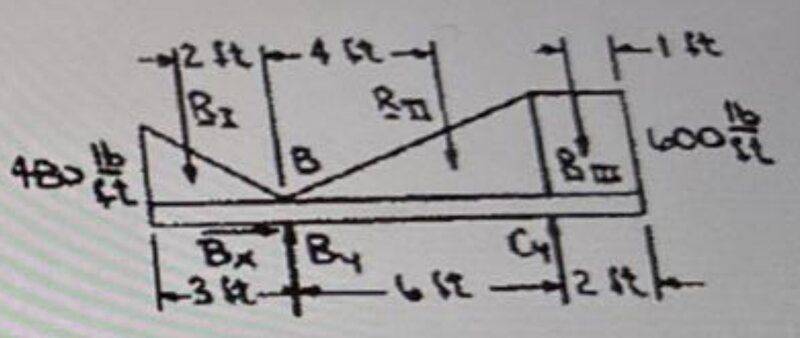
We have
$$R_I=\dfrac12 (3\, \textrm{ft})(480\, \textrm{lb}/\textrm{ft})=720\, \textrm{lb}$$
$$R_{II}=\dfrac12 (6\, \textrm{ft})(600\, \textrm{lb}/\textrm{ft})=1800\, \textrm{lb}$$
$$R_{III}=(2\, \textrm{ft})(600\, \textrm{lb}/\textrm{ft})=1200\, \textrm{lb}$$
Then
$$\xrightarrow{+}\sum F_x=0:\,\, B_x=0$$
$$\sum M_B=0:\,\, (2\, \textrm{ft})(720\, \textrm{lb})-(4\, \textrm{ft})(1800\, \textrm{lb})+(6\, \textrm{ft})C_y-(7\, \textrm{ft})(1200\, \textrm{lb})=0$$
$$C_y=2360\, \textrm{lb}\qquad \mathbf{C}=2360\, \textrm{lb} \uparrow$$
or
$$\sum F_y=0:\,\, -720\, \textrm{lb}+B_y-1800\, \textrm{lb}+2360\, \textrm{lb}-1200\, \textrm{lb}=0$$
$$B_y=1360\, \textrm{lb}\qquad \mathbf{B}=1360\, \textrm{lb}\uparrow$$

 

[erobz]

The effective loads are applied at the centroids of the areas. Check $x_2$

 

[Lnewqban]

The location that you have calculated for the centroid of A2 is not correct.
Much of the weight is located towards the right side of the 11-foot beam, therefore the calculated concentrated total weight should be located far from 5.84 feet from the left end.

 

[Guillem_dlc]

Of course, I have taken it as if the triangle is rotated. It should be $2/3$