How Are Trig Half-Angle Identities Derived from Basic Formulas?

[Nikitin]

Apparently our professor expects us to know these half-angle identities

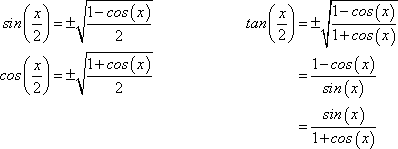
(http://www.purplemath.com/modules/idents.htm)

Without going through them in class or us learning them in high school..

Can somebody explain how these were derived? Does the derivation come from the angle-sum and difference identities?

 

[tiny-tim]

Hi Nikitin!

Your professor is right, you do need to learn these.

Does the derivation come from the angle-sum and difference identities?

Yes, have a go!

 

[Nikitin]

thx. With a bit of effort it wasn't that hard :)

 

[SammyS]

These are usually stated a bit differently:

For example, for sin²(x) = ½[1 – cos(2x)],

Taking the square root of both sides of the above identity, and letting θ = 2x, we have,

$\displaystyle \sin(\theta/2)=\pm\sqrt{\frac{1-\cos(\theta)}{2}}\,,$ where the ± sign indicates that you choose the correct sign depending upon the quadrant in which θ/2 lies.

Similar results hold for the other half-angle identities.

 

[HallsofIvy]

The fundamental identities are sin^2(a)+ cos^2(a)= 1, sin(a+ b)= sin(a)cos(b)+ cos(a)sin(b) and cos(a+ b)= cos(a)cos(b)- sin(a)sin(b). How you show those depends on exactly how you have defined "sine" and "cosine".

But from those cos(2a)= cos(a+ a)= cos^2(a)- sin^2(a). Of course, then, cos(2a)= cos^2(a)- (1- cos^2(a)= 2cos^2(a)- 1 and cos(2a)= (1- sin^2(a))- sin^2(a)= 1- 2sin^2(a).

From cos(2a)= 2cos^2(a)- 1, we have cos^2(a)= (1/2)(cos(2a)+ 1) so that $cos(a)= \pm\sqrt{(1/2)(cos(2a)+ 1)}$ and, setting b= 2a, $cos(b/2)= \pm\sqrt{(1/2)(cos(b)+ 1)}$.

From cos(2a)= 1- 2sin^2(a), we have sin^2(a)= (1/2)(1- cos(2a) so that [itex]sin(a)= \pm\sqrt{(1/2)(1- sin(2a)}[itex]and, setting b= 2a, $sin(b/2)= \pm\sqrt{(1/2)(cos(b)+ 1)}$. <br /> <br /> Whether we use + or - for a given b depends on the quadrant b/2 is in which is NOT given by cos(b).[/itex][/itex]