How Can I Accurately Fit an Airy Distribution Over Noisy Resonance Data?

[MatthijsRog]

Hi all,

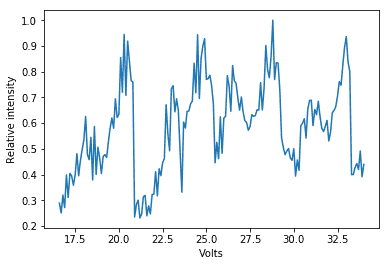
I performed a resonance experiment over the past two weeks, in which I collected the intensity of a Fabry-Perot cavity whilst adjusting the mirror distance with a piezo-element (the specific setup of the experiment is fairly detached from the question I will ask). My raw data is included in the figure:

The results should theoretically form an Airy-distribution as shown in the following figure:

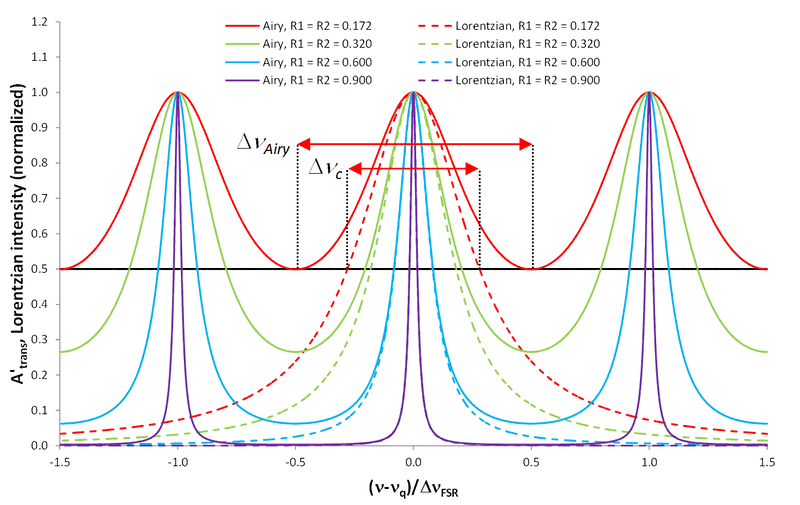
Mind that the dashed lines are NOT Airy-distributions. The Airy distribution is also given by

In the case of my experiment, R₁ and R₂ are known while the argument of the sine is a linear function of the x-axis.

While the resonance peaks are clearly visible in my data (they are even more or less at constant separation), I'm having trouble fitting a function over it. Because of the small "sub-peak" coming shortly before each major peak, the Scipy.optimize.curve_fit method keeps putting the Airy-distribution's peaks somewhere between the two.

Mind that I'm trying to perform the fit for specified R₁ and R₂ while trying out different linear functions (f(x) = ax + b) as the argument for the sine.

My question is this: how could I best go about fitting an Airy distribution over my data, staying as accurate and scientific as possible?

I could obviously make the fit by simply trying out different linear functions. But I could only get accurate on the horizontal positions of the peaks, not on the widths of the peaks.

However, I don't know how to manipulate my data to make it workable for a computer while staying scientific.

What would be the best to do in my case? Simply do it by hand?

 

[russ_watters]

It seems to me that the sub-peaks are a second resonance function. Can you just add two together? Or subtract/filter the second one out so you can focus on the bigger one?

 

[MatthijsRog]

It seems to me that the sub-peaks are a second resonance function. Can you just add two together? Or subtract/filter the second one out so you can focus on the bigger one?

It seemed like that to me as well.

From a qualitative point of view, what you see when you perform this experiment is a ring pattern "collapsing" into its center. The sub-peak is caused by the penultimate ring falling into the CCD-array's field of view.

I have yet to take my signal processing courses however. How would one go about performing such a filtering?

A dirty trick I found to only get the main peaks was to divide the data by its median value and then raise the values to a high power: this really sets apart the main peaks, but makes them much thinner, so performing a function fit on these plots is not useful.

 

[russ_watters]

A dirty trick I found to only get the main peaks was to divide the data by its median value and then raise the values to a high power: this really sets apart the main peaks, but makes them much thinner, so performing a function fit on these plots is not useful.

It does feel to me like that is a "dirty trick" that changes the data too much. It sounds like you are trying to have the computer do a curve fit for you and do only one curve fit without filtering out the second curve. I suggest you do the curve fit yourself at least for the smaller curve. You can identify the wavelength, amplitude and offset from the graph, build a function for it, and literally subract it from the main raw data. That will leave you with two sets of data instead of one. I don't know what software you are using, but you can easily do this in any spreadsheet program...of course, there is probably also signal processing software designed to find the individual curves automatically.

Here's an example of how to do it: wave 1 should be your raw data, wave 2 is your manually created curve and then just change the addition to subtraction.


Caveat: you may actually have three or more superimposed curves, as the smaller curve seems increase in amplitude for two peaks and then decrease for two peaks.

 

[MatthijsRog]

Thanks for the help! I'm using the Python language, by the way

The peaks were much broader than the reflectivity of my mirrors predicted, so instead of subtracting the sub-peaks (I couldn't find a broad enough Airy distribution to do that) I did it with a little detour. I found approximate Airy distributions for both peaks and then used a Python program to wiggle the distributions around until the area of difference between the data and the distributions was minimal.

The assumption I made was that both distributions have the same period.

My result is the following:

Looks okay enough, right?

 

[russ_watters]

My result is the following:

View attachment 225226

Looks okay enough, right?

It looks pretty good, but can you also show what adding them together yields?

[edit] I notice your data never goes below 0.2. Perhaps this is some sort of DC signal or noise floor (like dark noise, since you said this is a CCD). Can you add 0.2 to each of your functions for a better fit? That will make them shorter and broader.

 

[boneh3ad]

I'd also be careful calling this "noisy" data, as the signal to noise ratio here is clearly very high and the peaks you observe are not noise, but additional meaningful additional data that your simple theory just doesn't capture.

I agree that the sum of those two Airy distributions would be interesting. This also seems like a case where you might devise an integral transform based on Airy distributions as the kernel (as opposed to a Fourier transform, which uses sine waves as the kernel). In essence that's what you've done by fitting two Airy distributions to your data. You just went about it in a more roundabout way.

 

[MatthijsRog]

Sorry for the late reply!

It looks pretty good, but can you also show what adding them together yields?

[edit] I notice your data never goes below 0.2. Perhaps this is some sort of DC signal or noise floor (like dark noise, since you said this is a CCD). Can you add 0.2 to each of your functions for a better fit? That will make them shorter and broader.

The strange thing is that I already calibrated the CCD to at the very least filter out bias and dark noise. The only thing I can come up with is that the high intensity of the laser caused the CCD to warm up even further, which generated more dark noise.

What do you mean with adding 0.2 to the functions? Transposing them along the vertical axis?

Airy distributions are meant to not go to zero, but you are right that 0.2 is a little high.

I'll be going into the lab in a few minutes to take a look at the equipment one last time and try to figure it out.

I'd also be careful calling this "noisy" data, as the signal to noise ratio here is clearly very high and the peaks you observe are not noise, but additional meaningful additional data that your simple theory just doesn't capture.

Not sure if I agree. Note that my graph isn't raw data but the intensity of 175 separate measurements. It could very well be that I didn't integrate over the right domain, for example. I'll try out some different methods and come back.

I'll also add up the Airy distributions this afternoon and post it.

 

[ZapperZ]

Sorry for the late reply!
The strange thing is that I already calibrated the CCD to at the very least filter out bias and dark noise. The only thing I can come up with is that the high intensity of the laser caused the CCD to warm up even further, which generated more dark noise.

What do you mean with adding 0.2 to the functions? Transposing them along the vertical axis?

Airy distributions are meant to not go to zero, but you are right that 0.2 is a little high.

I'll be going into the lab in a few minutes to take a look at the equipment one last time and try to figure it out.

As was suggested to you, you need to ADD those two functions that you came up with. The SUM of those two will be the curve that you need to compare to your data.

Zz.

 

[MatthijsRog]

Which is why I promise to do that at the bottom of the message? :p