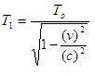- #1
crazynut52
- 11
- 0
I have the attached equation
but when I plug it, I don't get the same answer as in the back of the book...
Here is the question
Two observers, A on earth, B in a spacecraft whose speed is 2.0X10^8 m/s both set their watches to the same time, when the ship is abreast the earth.
How much time must elapse by A's reckoning before the watches differ by 1.00 seconds?
but when I plug it, I don't get the same answer as in the back of the book...
Here is the question
Two observers, A on earth, B in a spacecraft whose speed is 2.0X10^8 m/s both set their watches to the same time, when the ship is abreast the earth.
How much time must elapse by A's reckoning before the watches differ by 1.00 seconds?