- #1
Lambda96
- 223
- 75
- Homework Statement
- See Screenshot
- Relevant Equations
- none
Hi,
unfortunately, I have problems with the following task

I first tried to calculate ##JIJ^T##.
$$\left( \begin{array}{rrr}
\frac{\partial q'_i}{\partial q_j} & \frac{\partial q'_i}{\partial P_j} \\\frac{\partial P'_i}{\partial q_j} & \frac{\partial P'_i}{\partial P_j} \\
\end{array}\right)\left( \begin{array}{rrr}
0 & \textbf{1} \\\ -{\textbf{1}} & 0 \\
\end{array}\right)\left( \begin{array}{rrr}
\frac{\partial q'_i}{\partial q_j} & \frac{\partial P'_i}{\partial P_j} \\\frac{\partial P'_i}{\partial q_j} & \frac{\partial q'_i}{\partial P_j} \\
\end{array}\right)=\left( \begin{array}{rrr}
\frac{\partial q'_i}{\partial q_j} \textbf{1} \frac{\partial q'_i}{\partial P_j} -\frac{\partial q'_i}{\partial P_j} \textbf{1} \frac{\partial q'_i}{\partial q_j} & \frac{\partial q'_i}{\partial q_j} \textbf{1} \frac{\partial P_i}{\partial P_j} -\frac{\partial q'_i}{\partial P_j} \textbf{1} \frac{\partial P_i}{\partial q_j} \\
\frac{\partial P_i}{\partial q_j} \textbf{1} \frac{\partial q'_i}{\partial P_j} -\frac{\partial P_i}{\partial P_j} \textbf{1} \frac{\partial q'_i}{\partial q_j} & \frac{\partial P_i}{\partial q_j} \textbf{1} \frac{\partial P_i}{\partial P_j} -\frac{\partial P_i}{\partial P_j} \textbf{1} \frac{\partial P_i}{\partial q_j} \\
\end{array}\right)$$
##\textbf{1}## is supposed to be the unit matrix, but unfortunately I don't know how to write it with latex, which is why I have represented it in my calculation like this
Then I took the following relation from my professor, I hope you can read it well.
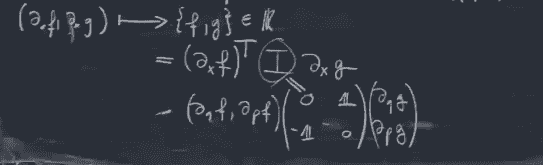
and get the following
$$\left( \begin{array}{rrr}
\Bigl\{ q'_i,q'_i \Bigr\} & \Bigl\{ q'_i,P_i \Bigr\} \\
\Bigl\{ P_i,q'_i \Bigr\} & \Bigl\{ P_i,P_i \Bigr\} \\
\end{array}\right)$$
Unfortunately, I am not getting anywhere now, because in order to show which values ##\alpha## and ##\beta## must assume in order for it to be a canonical transformation, I would have to get the symplectic unit matrix again, but with my calculation I would only get numbers as entries in the matrix and not unit matrices, as it should be.
My professor's script contains the following formulation
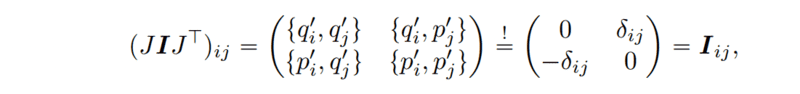
unfortunately, I have problems with the following task
I first tried to calculate ##JIJ^T##.
$$\left( \begin{array}{rrr}
\frac{\partial q'_i}{\partial q_j} & \frac{\partial q'_i}{\partial P_j} \\\frac{\partial P'_i}{\partial q_j} & \frac{\partial P'_i}{\partial P_j} \\
\end{array}\right)\left( \begin{array}{rrr}
0 & \textbf{1} \\\ -{\textbf{1}} & 0 \\
\end{array}\right)\left( \begin{array}{rrr}
\frac{\partial q'_i}{\partial q_j} & \frac{\partial P'_i}{\partial P_j} \\\frac{\partial P'_i}{\partial q_j} & \frac{\partial q'_i}{\partial P_j} \\
\end{array}\right)=\left( \begin{array}{rrr}
\frac{\partial q'_i}{\partial q_j} \textbf{1} \frac{\partial q'_i}{\partial P_j} -\frac{\partial q'_i}{\partial P_j} \textbf{1} \frac{\partial q'_i}{\partial q_j} & \frac{\partial q'_i}{\partial q_j} \textbf{1} \frac{\partial P_i}{\partial P_j} -\frac{\partial q'_i}{\partial P_j} \textbf{1} \frac{\partial P_i}{\partial q_j} \\
\frac{\partial P_i}{\partial q_j} \textbf{1} \frac{\partial q'_i}{\partial P_j} -\frac{\partial P_i}{\partial P_j} \textbf{1} \frac{\partial q'_i}{\partial q_j} & \frac{\partial P_i}{\partial q_j} \textbf{1} \frac{\partial P_i}{\partial P_j} -\frac{\partial P_i}{\partial P_j} \textbf{1} \frac{\partial P_i}{\partial q_j} \\
\end{array}\right)$$
##\textbf{1}## is supposed to be the unit matrix, but unfortunately I don't know how to write it with latex, which is why I have represented it in my calculation like this
Then I took the following relation from my professor, I hope you can read it well.
and get the following
$$\left( \begin{array}{rrr}
\Bigl\{ q'_i,q'_i \Bigr\} & \Bigl\{ q'_i,P_i \Bigr\} \\
\Bigl\{ P_i,q'_i \Bigr\} & \Bigl\{ P_i,P_i \Bigr\} \\
\end{array}\right)$$
Unfortunately, I am not getting anywhere now, because in order to show which values ##\alpha## and ##\beta## must assume in order for it to be a canonical transformation, I would have to get the symplectic unit matrix again, but with my calculation I would only get numbers as entries in the matrix and not unit matrices, as it should be.
My professor's script contains the following formulation