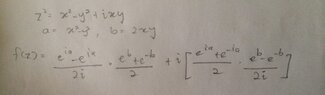- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How can I express f(z) in terms of z using exponentials?
- MHB
- Thread starter aruwin
- Start date
-
- Tags
- Terms
In summary, if you want to solve for x+iy using exponentials, you would need to solve for z first and then use the quadratic formula to solve for x and y.
Physics news on Phys.org
- #2
Prove It
Gold Member
MHB
- 1,465
- 24
aruwin said:Hello! I am stuck at the final step. How do I get x+iy from the equation? Help!
I am so sorry for posting this question in a picture instead of writing it out, because I don't know how to write equations on here.
First, I would note that if $\displaystyle \begin{align*} z = x + \mathrm{i }\,y \end{align*}$ then $\displaystyle \begin{align*} z^2 = x^2 - y^2 + \mathrm{i }\left( 2\,x\,y \right) \end{align*}$, so $\displaystyle \begin{align*} x^2 - y^2 = \mathcal{R} \left( z^2 \right) \end{align*}$ and $\displaystyle \begin{align*} 2\,x\,y = \mathcal{I}\left( z^2 \right) \end{align*}$.
Next, notice that $\displaystyle \begin{align*} \sin{ \left( X + \mathrm{i}\,Y \right) } = \sin{(X)}\cosh{(Y)} + \mathrm{i}\cos{(X)}\sinh{(Y)} \end{align*}$, so it would suggest that $\displaystyle \begin{align*} X = x^2 - y^2 = \mathcal{R} \left( z^2 \right) \end{align*}$ and $\displaystyle \begin{align*} Y = 2\,x\,y = \mathcal{I} \left( z^2 \right) \end{align*}$.
Thus, we can conclude that $\displaystyle \begin{align*} f(z) = \sin{ \left( z^2 \right) } \end{align*}$.
- #3
aruwin
- 208
- 0
Prove It said:First, I would note that if $\displaystyle \begin{align*} z = x + \mathrm{i }\,y \end{align*}$ then $\displaystyle \begin{align*} z^2 = x^2 - y^2 + \mathrm{i }\left( 2\,x\,y \right) \end{align*}$, so $\displaystyle \begin{align*} x^2 - y^2 = \mathcal{R} \left( z^2 \right) \end{align*}$ and $\displaystyle \begin{align*} 2\,x\,y = \mathcal{I}\left( z^2 \right) \end{align*}$.
Next, notice that $\displaystyle \begin{align*} \sin{ \left( X + \mathrm{i}\,Y \right) } = \sin{(X)}\cosh{(Y)} + \mathrm{i}\cos{(X)}\sinh{(Y)} \end{align*}$, so it would suggest that $\displaystyle \begin{align*} X = x^2 - y^2 = \mathcal{R} \left( z^2 \right) \end{align*}$ and $\displaystyle \begin{align*} Y = 2\,x\,y = \mathcal{I} \left( z^2 \right) \end{align*}$.
Thus, we can conclude that $\displaystyle \begin{align*} f(z) = \sin{ \left( z^2 \right) } \end{align*}$.
Thanks! This is a faster method than using exponentials. But if I were to use exponentials, how do I do it? I got stuck here, look.
Attachments
FAQ: How can I express f(z) in terms of z using exponentials?
What does "expressing f(z) in terms of z" mean?
This means rewriting the function f(z) in a form that only includes the variable z, without any other variables or constants.
Why is it important to express f(z) in terms of z?
Expressing a function in terms of its independent variable can make it easier to analyze and understand the behavior of the function.
How do I express f(z) in terms of z?
This process involves algebraically manipulating the given function to isolate the variable z on one side of the equation. This may require using properties of exponents or logarithms, as well as factoring and simplifying.
Can any function be expressed in terms of z?
Yes, any function can be expressed in terms of its independent variable z. However, the resulting expression may not always be simple or easy to work with.
Are there any limitations to expressing f(z) in terms of z?
The limitations depend on the complexity of the given function. Some functions may not have a simple form in terms of z, while others may require advanced techniques such as Taylor series expansions.
Similar threads
- Replies
- 5
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 4
- Views
- 4K
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 24
- Views
- 5K
- Replies
- 17
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 4
- Views
- 1K
Share: