How can I find the torque/moment of force about an axis?

[GaussianSurface]

Homework Statement

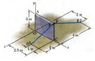
The Trump's wall is so weak that has to be supported by two cables as is shown in the figure. If the tension over the cables BD and FE are 900 N and 675 N respectively.

(I'LL UPLOAD AN IMAGE OF THE PROBLEM SO YOU CAN SEE IT)

Homework Equations

τ = r χ F
Mo = r χ F

The Attempt at a Solution

e= unitary vector
ra= 1.5i + 2j + 2k
ιeι= √1.5^2+2^2+2^2
ιeι= 3.20

e= 0.46i + 0.62j + 0.62k
............
F= 900(0.46i+0.62+0.62k)
F= 414i+558j+558k)

and by performing the determinant of the torque

T= r χ F
T= 9k - 9j

That's what I got by doing it but i don't really know if I'm okay. Hope someone can help me

 

[NFuller]

The Trump's wall is so weak that has to be supported by two cables as is shown in the figure.

It was only a matter of time before these types of problems started showing up.

T= 9k - 9j

I don't think this answer is correct. I'm also not sure what the unit vector you are calculating is for.

Since the torque is given by $\tau=\mathbf{r}\times\mathbf{F}$, we first need to find the vectors $\mathbf{r}$ and $\mathbf{F}$. Can you show what you get for these?

 

[GaussianSurface]

It was only a matter of time before these types of problems started showing up.

I don't think this answer is correct. I'm also not sure what the unit vector you are calculating is for.

Since the torque is given by $\tau=\mathbf{r}\times\mathbf{F}$, we first need to find the vectors $\mathbf{r}$ and $\mathbf{F}$. Can you show what you get for these?

I wrote it above
the r what I got was 1.5i + 2j + 2 k
and the force we know that in order to compute this is the module of F by the unitary vector ''e''
then F= ιFι e
since I've got F which is equal to 900 I just got to multiply by the unitary vector which is defined by the formula of e= e/ιeι
P.S: I don't know how to write absolute values so I try as much as I can so the problem can be well specified.

 

[GaussianSurface]

It was only a matter of time before these types of problems started showing up.

I don't think this answer is correct. I'm also not sure what the unit vector you are calculating is for.

Since the torque is given by $\tau=\mathbf{r}\times\mathbf{F}$, we first need to find the vectors $\mathbf{r}$ and $\mathbf{F}$. Can you show what you get for these?

Haha I live in Mexico and my teacher is kinda funny with this problems he knows how to make problems LOL

 

[NFuller]

the r what I got was 1.5i + 2j + 2 k

There is no $\hat{k}$ component for $\mathbf{r}$.

and the force we know that in order to compute this is the module of F by the unitary vector ''e''
then F= ιFι e

I see. The unit vector $\mathbf{e}$ is not quite right. The $\hat{i}$ and $\hat{j}$ components should have the same magnitude but $\hat{i}$ needs to be negative.

 

[GaussianSurface]

There is no $\hat{k}$ component for $\mathbf{r}$.

I see. The unit vector $\mathbf{e}$ is not quite right. The $\hat{i}$ and $\hat{j}$ components should have the same magnitude but $\hat{i}$ needs to be negative.

Damn, then it'd be like this?

r = -1.5 i + 2 j ?
or
r = -2 i + 2 j ?
what i do not know is if I am going to substract the meter to the 2.5, please tell me if that is okay or what...

 

[NFuller]

The components of $\mathbf{r}$ are composed of the distance in x and distance in y it takes to go from the point $O$ to the point $B$.

 

[GaussianSurface]

The components of $\mathbf{r}$ are composed of the distance in x and distance in y it takes to go from the point $O$ to the point $B$.

Mmm i think i got it so:

r = -2.5i + 2j

and then i can find the module of r and then the unitary vector so next i can perform the determinant and i'll got the torque?

 

[NFuller]

r = 2.5i + 2j

This looks good. Now what is your result for $\mathbf{e}$?

 

[GaussianSurface]

This looks good. Now what is your result for $\mathbf{e}$?

The module will be
r= √6.25+4 = 3.20
e= -0.78i + 0.62j
am I right?
because i actually did one like this but i thought i was wrong even though my components were wrong LOL

 

[NFuller]

$\mathbf{e}$ points in the direction of the cable. So it will have all three components $\hat{i}$, $\hat{j}$, and $\hat{k}$. To find $\mathbf{e}$, find the vector that points from $B$ to $D$ then divide it by the length of the vector.

 

[GaussianSurface]

$\mathbf{e}$ points in the direction of the cable. So it will have all three components $\hat{i}$, $\hat{j}$, and $\hat{k}$. To find $\mathbf{e}$, find the vector that points from $B$ to $D$ then divide each compo

e= 1i - 2j + 4k ?
and the i divide

 

[NFuller]

The vector pointing down the length of the cable is $-1\hat{i}-2\hat{j}+2\hat{k}$ now divide this vector by its length to get $\mathbf{e}$.

 

[haruspex]

r = -1.5 i + 2 j ?

You are switching between +1.5i and -1.5i. Which way are you defining the i axis? Is the direction OC positive or negative?

find the module of r and then the unitary vector

Why are you finding the modulus of the r vector? You want the unit vector in the force direction in order to find the vector F.

 

[GaussianSurface]

The vector pointing down the length of the cable is $-1\hat{i}-2\hat{j}+2\hat{k}$ now divide this vector by its length to get $\mathbf{e}$.

e = -0.32i - 0.62j + 0.62k
then i can multply e by the force
so then, i'll be able to perform the derminant right? since i got r and F

 

[GaussianSurface]

You are switching between +1.5i and -1.5i. Which way are you defining the i axis? Is the direction OC positive or negative?

Why are you finding the modulus of the r vector? You want the unit vector in the force direction in order to find the vector F.

Well, my teacher told me to find the module so i can find the e

 

[NFuller]

e = -0.32i - 0.62j + 0.62k

Something is still not right. You need to divide by the length of the vector which is $\sqrt{(-1)^{2}+(-2)^{2}+(2)^{2}}$.

 

[GaussianSurface]

Well, my teacher told me in order to find the module of it

Something is still not right. You need to divide by the length of the vector which is $\sqrt{(-1)^{2}+(-2)^{2}+(2)^{2}}$.

You mean the module, right?

 

[haruspex]

Well, my teacher told me to find the module so i can find the e

Yes, but you were finding e of the wrong vector. In post #10 you found the modulus of the r vector, which is not helpful. You want the unit vector in the direction of the force.
I see NFuller put you on the right track in post #11.

 

[GaussianSurface]

You mean the module, right?

e= -1/√5 -2/√5+2/√5

 

[haruspex]

e= -1/√5 -2/√5+2/√5

I do not think you are using the terminology correctly, and the √5 is wrong.
Given a vector (-1,-2,2), its modulus (not module) is √((-1)²+(-2)²+2²)=3. This is a scalar.
The e vector would mean the unit vector in the direction of the original vector, and that is obtained by dividing by the modulus, giving (-1/3,-2/3,2/3).

 

[NFuller]

e= -1/√5 -2/√5+2/√5

You need to put the unit vectors in. The magnitude is not $\sqrt{5}$ it is 3 as haruspex said.

 

[haruspex]

Yes, that's right.

No it is not. Please see post #21.

 

[NFuller]

No it is not. Please see post #21.

Yes sorry, I just corrected my post