How can I locate the coordinates of the centroid of a cone in Z?

[Tapias5000]

Homework Statement

Locate the centroid Z of the homogeneous solid that is formed by rotating the area formed by rotating the area shaded in blue with respect to the z-axis. the z-axis.

Relevant Equations

$\overline{z}=\frac{\int _{ }^{ }\tilde{z}dA}{\int _{ }^{ }dA}$

$A_b=πr^2$

This is the picture of the problem.

My solution is:

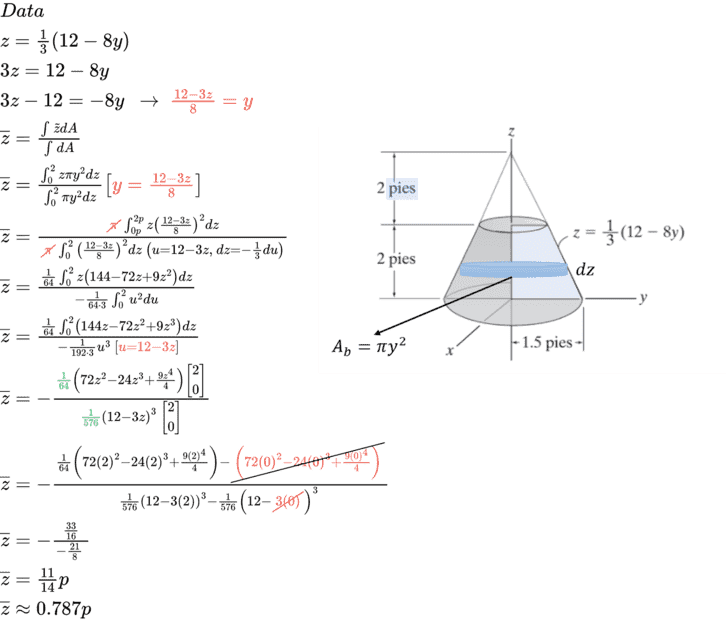
I'm not sure if the limit is 0 to 2 or 0 to 4...

 

[haruspex]

I'm not sure if the limit is 0 to 2 or 0 to 4...

Would your expressions for the integrands be valid above z=2?

There is a way to solve it without calculus if you know the formula for the centroid of a cone.

 

[Tapias5000]

Would your expressions for the integrands be valid above z=2?

ummm I don't understand what you mean by this, could you give me another example?

There is a way to solve it without calculus if you know the formula for the centroid of a cone.

I saw that there were several formulas depending on the case, but I doubt that my professor would like me to use them.

 

[haruspex]

could you give me another example?

The denominator in your fifth equation gives the volume as $\int_0^2\pi y^2dz$. That is based on an element thickness dz at height z having volume $\pi y^2dz$.
In the figure, does the solid have a volume element of that size between $z$ and $z+dz$ for all z in $(0,4)$?

there were several formulas depending on the case, but I doubt that my professor would like me to use them.

Yes, it can be hard knowing which standard results you are allowed to quote. But students would be expected to know the formula for the simplest case, and that is all you need here. The method to get from the simplest case to this more general one is certainly worth knowing. Do you see how to do it?

 

[Tapias5000]

The denominator in your fifth equation gives the volume as $\int_0^2\pi y^2dz$. That is based on an element thickness dz at height z having volume $\pi y^2dz$.
In the figure, does the solid have a volume element of that size between $z$ and $z+dz$ for all z in $(0,4)$?

Hmm, the problem tells us to locate the centroid of the area shaded in blue in Z, and according to the figure that is a known data from 0 to 2, right?

Yes, it can be hard knowing which standard results you are allowed to quote. But students would be expected to know the formula for the simplest case, and that is all you need here. The method to get from the simplest case to this more general one is certainly worth knowing. Do you see how to do it?

There are several formulas, so I would not know which one to apply here.

 

[haruspex]

the problem tells us to locate the centroid of the area shaded in blue in Z,

Yes, but you asked what the bounds should be on the integrations, (0,2) or (0,4).
The range of integration should not extend beyond where the expression for the integrand represents a contribution to the desired total. In the region z>2, are there volume elements contributing to the total volume of the shaded region? If not, the range should stop at 2.

There are several formulas

Of which the simplest is that for a conical form extending from a plane base to a point the distance of the mass centre from the base is 1/4 the distance of the point from the base.
Can you see how to use that here to get the answer quickly?

 

[Tapias5000]

Yes, but you asked what the bounds should be on the integrations, (0,2) or (0,4).
The range of integration should not extend beyond where the expression for the integrand represents a contribution to the desired total. In the region z>2, are there volume elements contributing to the total volume of the shaded region? If not, the range should stop at 2.

aaa already understand.

Of which the simplest is that for a conical form extending from a plane base to a point the distance of the mass centre from the base is 1/4 the distance of the point from the base.
Can you see how to use that here to get the answer quickly?

you mean the formula $h / 4$?
If I replace values I do not get the same result so I assume that I am missing some concept
If you solve the integral in the form of its symbols, I will obtain the "formula" for this case, right?

 

[haruspex]

you mean the formula h/4?
If I replace values I do not get the same result so I assume that I am missing some concept

Yes. The concept is finding the mass centre of an object by representing it as the sum or difference of simpler objects.
In this case, the object is the difference between two complete cones.
You can write down where the mass centre of each complete cone is, and you know their relative masses.
Can you take it from there?

 

[Tapias5000]

Yes. The concept is finding the mass centre of an object by representing it as the sum or difference of simpler objects.
In this case, the object is the difference between two complete cones.
You can write down where the mass centre of each complete cone is, and you know their relative masses.
Can you take it from there?

no, I really couldn't understand it, can you show me a different example?

 

[Tapias5000]

no, I really couldn't understand it, can you show me a different example?

Should I look up the definition of the center of mass for a cone?

 

[haruspex]

Should I look up the definition of the center of mass for a cone?

The definition of the centre of mass does not depend on the shape. Do you mean the formula for the center of mass for a cone? It's one quarter of the way from the base to the tip.
Suppose you had two cubes of the same material but different sizes, 1x1x1 sitting centrally on a 2x2x2 say. Could you work out where the mass centre of the combination is?

 

[Tapias5000]

The definition of the centre of mass does not depend on the shape. Do you mean the formula for the center of mass for a cone? It's one quarter of the way from the base to the tip.
Suppose you had two cubes of the same material but different sizes, 1x1x1 sitting centrally on a 2x2x2 say. Could you work out where the mass centre of the combination is?

damn I suck at this lmao
I think it's better if I just give up and that's it.

Do you have any video on yt that you can share with me to illustrate what you mean?

 

[haruspex]

damn I suck at this lmao
I think it's better if I just give up and that's it.

Do you have any video on yt that you can share with me to illustrate what you mean?

For the two cubes problem, take moments about a point in the middle of the base of the lower cube. The result should be the same treating it as one object or two.
The masses of the cubes are 1 and 8 for a total of 9. The mass centre heights are 1 and 2.5. The combined moment is 1x2.5+8x1=11.5.
If the overall mass centre is height Y then 11.5=9Y, so Y=11.5/9.
The frustrated cone in the problem in post 1 can be represented as the difference of two cones.
Can you take it from there?