How can I prove the sine theorem?

[rado5]

Homework Statement

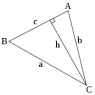
How can I prove this theorem in the triangle ABC? sin(A)/a=sin(B)/b=sin(C)/c

Homework Equations

A*B and ...

The Attempt at a Solution

I have drawn a triangle and tried to prove it, but i couldn't. (I don't know how to send a picture to my post!) I know how to prove the cosine theorem but i can't prove the sine theorem.

 

[rado5]

Oh thank you. But I could easily find the solution at wikipedia. At this address: http://en.wikipedia.org/wiki/Law_of_sines in the "Derivation" section.

 

[Pagan Harpoon]

Consider the three vectors A to B, B to C and C to A. Now consider geometrically their cross products. The magnitude of each is equal to twice the area of the triangle, so the three are equal.

 

[Gib Z]

I particularly like this one:

For any triangle, inscribe it in a circle. So the triangle touches the circle at 3 points, call them A, B, and C, and their corresponding angles a, b, and c, and the lengths of the sides opposite them L(a), L(b), L(c).

Move point A along the circumference so that AB passes the center of the circle. Angles subtended by equal chords onto the circumference are equal, so angle BAC is still a.

Now we have a triangle in a semi circle, and so angle ACB is equal to 90 degrees. By trigonometry, sin a = L(a)/Diameter, and so Diameter = sin a/L(a)

Making similar transformations for the other sides shows sin b/L(b) and sin c/L(c) are also equal to the diameter, and hence equal to each other.

 

[rado5]

Oh, thank you very much really.