- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
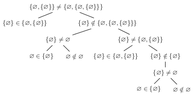
Could you give me a hint how I can show that the sets:
$$\{ \varnothing, \{ \varnothing \} \} , \ \ \ \{ \varnothing, \{ \varnothing, \{ \varnothing \} \} \}, \ \ \ \{ \{ \varnothing \}, \{ \varnothing, \{ \varnothing \} \} \}$$
are pairwise disjoint=are not equal ?
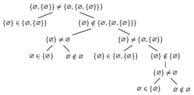
Could you give me a hint how I can show that the sets:
$$\{ \varnothing, \{ \varnothing \} \} , \ \ \ \{ \varnothing, \{ \varnothing, \{ \varnothing \} \} \}, \ \ \ \{ \{ \varnothing \}, \{ \varnothing, \{ \varnothing \} \} \}$$
are pairwise disjoint=are not equal ?