How Can I Solve a Problem Using Euler's Totient Function for Odd Prime Numbers?

[goody1]

Hello everyone, can anybody help me with this problem?

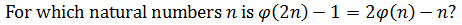
The solution is for all odd prime numbers, but I have no idea how to solve it.
Any help will be greatly appreciated.

 

[GJA]

Hi goody,

Let's take this one step at a time by first looking at the right hand side, then the left hand side for odd primes. We will worry about the non-odd prime case later.

Let's think of some examples first. What is the value of $\varphi(5)$? How about $\varphi(7)$ and $\varphi(11)$? Can you see a general rule emerging from these examples? Now, if $n$ is an odd prime, what should the value of $\varphi(n)$ be? In other words, how many numbers less than $n$ do not share a common divisor with $n$?