goody1
- 16
- 0
I need to solve this limit without L'Hôpital's rule. Could someone give me a hint what
I need to do please? I just can't find this algebraic trick. Thank you in advance!
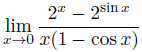
I need to do please? I just can't find this algebraic trick. Thank you in advance!