How Can I Visualize a $\pi/2$ Rotation About $(1,1,0)^t$ in $\mathbb{R}^3$?

[kalish1]

I am trying to visualize the following rotation of $\mathbb R^3$, but it is very difficult. I want to get the answer by intuition, and not by using the Rodrigues rotation formula or conjugation of matrices, etc.

Help please.

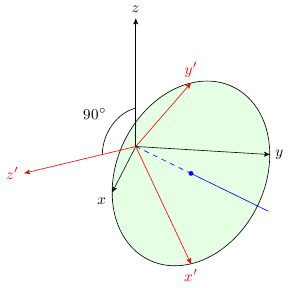
**Problem statement:** Determine the matrix that represents the following rotation of $\mathbb R^3$: an angle of $\pi/2$ about the fixed axis containing the vector $(1,1,0)^t$

Here is what I have tried in my diagram:

![Coordinate axes][1]

Should I find a 3x3 rotation matrix $A$ such that $A(1,1,0)^t=(-1,1,0)^t$?

[1]:
View attachment 1648

 

[I like Serena]

Should I find a 3x3 rotation matrix $A$ such that $A(1,1,0)^t=(-1,1,0)^t$?

The axis is invariant, so that should be $A(1,1,0)^t=(1,1,0)^t$ instead.

You already found a perpendicular vector (-1,1,0).
You need a 3rd vector that is perpendicular to both the axis and this one, completing an orthogonal set.
And more specifically, a vector that "turns" in the right direction.
You can find it by calculating the cross product of (1,1,0) and (-1,1,0), yielding (0,0,2).

That gives you the set of equations (note that the vectors must have equal lengths):
$$A(1,1,0)^t=(1,1,0)^t$$
$$A(-1,1,0)^t=(0,0,\sqrt 2)^t$$
$$A(0,0,\sqrt 2)^t=(1,-1,0)^t$$

Or in matrix form:
$$A \begin{bmatrix}
1 & -1 & 0 \\
1 & 1 & 0 \\
0 & 0 & \sqrt 2
\end{bmatrix} = \begin{bmatrix}
1 & 0 & 1 \\
1 & 0 & -1 \\
0 & \sqrt 2 & 0
\end{bmatrix}$$
Solve for A.
This is easiest to do by performing matrix operations on the right that execute a gaussian elimination, ending up with an identity matrix on the left and the actual A matrix on the right.
That is, subtract multiples of one column from another, both left and right.
And swap columns, both left and right.

 

[Evgeny.Makarov]

Here is a picture.

It is done using TikZ package 3dplot.

 

[I like Serena]

Perhaps noteworthy for visualization is that (-1,1,0) is rotated onto the positive z-axis,
which is in turn rotated to (1,-1,0).