- #1
knight92
- 101
- 0
Hi I want to derive a natural frequency equation for a system. I saw this question in a book.
so they gave us an equation
frequency = (1/2pi) * ( sqrt( k/m1+m2+m3/3+4m4+Ic/r2) )
Ic = Moment of inertia of pulley about rotational axis
r = effective radius of pulley
k = spring constant
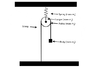
now the question says that I have to derive this equation from Newtons second law f=ma (The body is pulled down a bit and left to oscillate). I have done that no problem but I don't get why mass m3 which is the mass of the spring is divided by 3 and mass m4 which is mass of the body is multiplied by 4. Can anyone help ? I have attached an image of the setup that I drew on photoshop, I don't have a scanner so I can't scan and upload the original diagram itself sorry. In the Second image the pulley is rotated clockwise and left to oscillate/rotate 10 times to calculate moment of inertia
so they gave us an equation
frequency = (1/2pi) * ( sqrt( k/m1+m2+m3/3+4m4+Ic/r2) )
Ic = Moment of inertia of pulley about rotational axis
r = effective radius of pulley
k = spring constant
now the question says that I have to derive this equation from Newtons second law f=ma (The body is pulled down a bit and left to oscillate). I have done that no problem but I don't get why mass m3 which is the mass of the spring is divided by 3 and mass m4 which is mass of the body is multiplied by 4. Can anyone help ? I have attached an image of the setup that I drew on photoshop, I don't have a scanner so I can't scan and upload the original diagram itself sorry. In the Second image the pulley is rotated clockwise and left to oscillate/rotate 10 times to calculate moment of inertia
Attachments
Last edited: