Aurelius120
- 269
- 24
- TL;DR Summary
- Confusion regarding phasors and a proof on why scalars can be added like vectors and still give correct answers. Especially in ##L-C-R## circuits connected to Alternating Current.
So we learnt about the different types of circuits and their behaviour when connected to an alternating current source.
(DC was treated as an AC with 0 frequency and/or infinte time period).
For purely inductive and purely capacitive circuits we were shown the derivation and why things are the way they are.
Then came Series L-C-R circuit.
In this they said that:
For an AC source,
##V=V_○\sin(\omega t)## which is the equation of a wave.
So to make calculations easier, "We treat them as vectors".
$$\vec{V}=\vec{V_{R}}+\vec{V_{L}}+\vec{V_{C}}$$
Then this
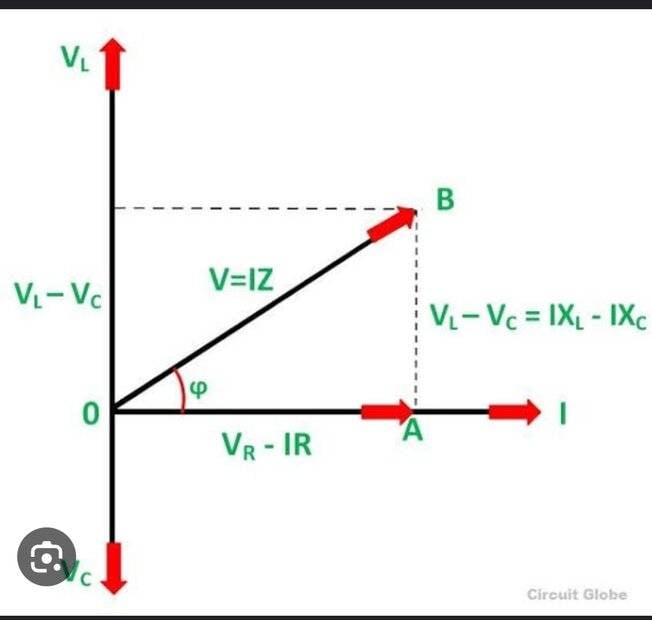
And this
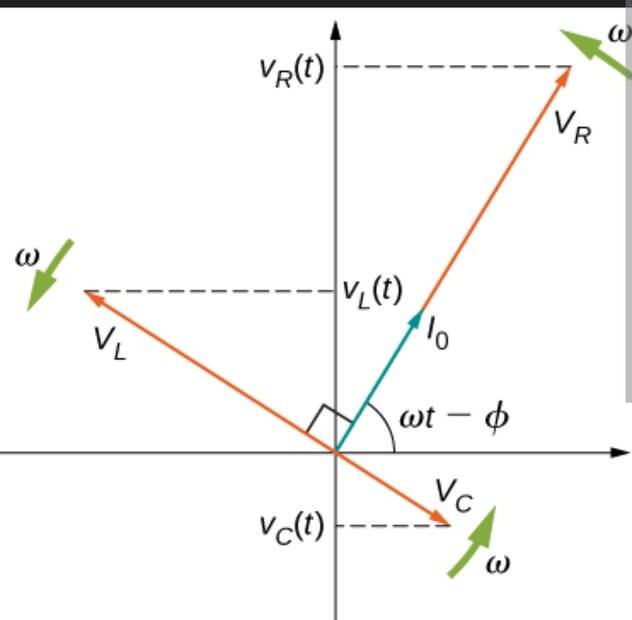
And finally these:
$$V=\sqrt{V_R^2+(V_L-V_C)^2}$$
$$Z=\sqrt{R^2+(X_L-X_C)^2}$$
$$\tan\phi=\frac{|V_L-V_C|}{V_R}=\frac{|X_L-X_C|}{R}$$
And then we moved to question solving.
But all of this doesn't make a scalar quantity a vector quantity(that was just an assumption to make things easier)
The best explanation I got was that it is the way it is and adding them as ##V=V_R+V_L-V_C## gives wrong answers.
So I tried to add them like the scalars they are and subsequently obtain/prove the vector equations from that. But I couldn't do it.
Can you provide an explanation and/or proof of what happens that makes scalar additions (in reality) give same answers as vector addition (an assumption for ease of calculations)?
A similar thing is observed with amplitude of waves in superposition and got no explanations there either.
(DC was treated as an AC with 0 frequency and/or infinte time period).
For purely inductive and purely capacitive circuits we were shown the derivation and why things are the way they are.
Then came Series L-C-R circuit.
In this they said that:
For an AC source,
##V=V_○\sin(\omega t)## which is the equation of a wave.
So to make calculations easier, "We treat them as vectors".
$$\vec{V}=\vec{V_{R}}+\vec{V_{L}}+\vec{V_{C}}$$
Then this
And this
And finally these:
$$V=\sqrt{V_R^2+(V_L-V_C)^2}$$
$$Z=\sqrt{R^2+(X_L-X_C)^2}$$
$$\tan\phi=\frac{|V_L-V_C|}{V_R}=\frac{|X_L-X_C|}{R}$$
And then we moved to question solving.
But all of this doesn't make a scalar quantity a vector quantity(that was just an assumption to make things easier)
The best explanation I got was that it is the way it is and adding them as ##V=V_R+V_L-V_C## gives wrong answers.
So I tried to add them like the scalars they are and subsequently obtain/prove the vector equations from that. But I couldn't do it.
Can you provide an explanation and/or proof of what happens that makes scalar additions (in reality) give same answers as vector addition (an assumption for ease of calculations)?
A similar thing is observed with amplitude of waves in superposition and got no explanations there either.