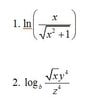MHB How can the properties of logarithms be used to simplify and solve equations?

AI Thread Summary
The discussion focuses on using properties of logarithms to simplify expressions and solve equations. Participants are encouraged to express logarithmic equations as sums, differences, or multiples of logarithms. One user successfully simplified an expression to "lnx - 1/2ln(x^2+1)" but struggles with another problem involving a denominator and a product in the numerator. The conversation emphasizes the need for clarity on handling logarithmic properties in various scenarios. Overall, the thread highlights common challenges and encourages collaborative problem-solving in logarithmic simplification.
schooler
Messages
4
Reaction score
0
Use the properties of Logarithms to write the expression as a sum, difference, and/or constant multiple of logarithms:
View attachment 2253
 

Attachments

  • 7.JPG
    7.JPG
    3.9 KB · Views: 92
Mathematics news on Phys.org
What have you tried? Where are you stuck?
 
Ackbach said:
What have you tried? Where are you stuck?

For the first one I did " lnx-1/2ln(x^2+1)"

For the second one, I have no idea what to do :(
 
What should you do with the denominator? How about the product in the numerator?
 

Thread 'Trigonometry problem of interest'

Seemingly by some mathematical coincidence, a hexagon of sides 2,2,7,7, 11, and 11 can be inscribed in a circle of radius 7. The other day I saw a math problem on line, which they said came from a Polish Olympiad, where you compute the length x of the 3rd side which is the same as the radius, so that the sides of length 2,x, and 11 are inscribed on the arc of a semi-circle. The law of cosines applied twice gives the answer for x of exactly 7, but the arithmetic is so complex that the...
View full post »

Similar threads

B How to express ##3^{\sqrt(2)}## in terms of natural logarithms
Replies
10
Views
1K
MHB Logarithmic Equation solve log_(3x)3+log_(x/3)3=5/12
Replies
1
Views
1K
I Transforming an equation with logarithms
Replies
2
Views
1K
B How does one draw a logarithmic scale?
Replies
20
Views
4K
B Issue With Algebra of Logarithms
Replies
8
Views
1K
MHB Solving for an exponential equation using logarithms 16^{x}-5(4)^{x}-6=0
Replies
3
Views
2K
Can I Use Logarithms to Solve Exponential Equations?
Replies
7
Views
2K
MHB How do I Solve a Basic Logarithm Problem?
Replies
5
Views
2K
Logarithmic Regression Question (TI-84 Plus Graphing Calculator)
Replies
4
Views
2K
MHB Solving Logarithmic Equations: Expert Help with Different Bases
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top