How can we avoid making simple typos in math problems?

[karush]

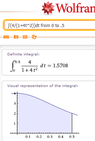
Compute

$\displaystyle\int_0^\frac{1}{2}\frac{4}{1-4t^2}dt$

Thot I could solve by using the log rule for integration namely:

$\displaystyle\int\frac{u'}{u} = ln|u|+C$

for such $u=1-4t^2$ and $u'=-8t$

but then $\displaystyle\frac{1}{2}\int_0^\frac{1}{2}\frac{-8t}{1-4t^2}dt$ isn't going to work due to the t in the numerator...so what shud I do...

 

[MarkFL]

I would consider a partial fraction decomposition on the integrand.(Wink)

edit: The Heaviside cover-up method will be easy to apply in this case.

 

[karush]

by the way the answer to this is $\frac{\pi}{2}$

 

[Jameson]

MarkFL beat me to it!

If you need help setting up things up then let us know, but the solution to the indefinite integral (which you'll calculate before applying the bounds) contains two terms so you'll need to decompose this into two fractions with degree of $x^1$ in each of their denominators.

 

[karush]

is the log rule the way to go on this.

I am not committed to use it... just thot that was the button to push...

yes not sure how you break of rational function when the numerator is $-8t$

 

[MarkFL]

by the way the answer to this is $\frac{\pi}{2}$

If that's the case then you mean:

$\displaystyle \int_0^{\frac{1}{2}}\frac{4}{1+4t^2}\,dt$

The integral you gave does not converge.

 

[karush]

yes the given is that but I could not apply the log rule to it or thot I couldn't

 

[Jameson]

karush,

Your set up for u-substitution (or t-substitution) wasn't correct. Those integrals are not equivalent at all.

You need to break [math]\frac{4}{1-4t^2}[/math] into [math]\frac{A}{1-2t}+\frac{B}{1+2t}[/math] by setting them equal to each other and solving for A and B.

 

[karush]

You need to break [math]\frac{4}{1-4t^2}[/math] into [math]\frac{A}{1-2t}+\frac{B}{1+2t}[/math] by setting them equal to each other and solving for A and B.

do you mean this: $\frac{A}{1-2t}=\frac{B}{1+2t}$ that looks like it will be very complicated for A and B

 

[Jameson]

do you mean this: $\frac{A}{1-2t}=\frac{B}{1+2t}$ that looks like it will be very complicated for A and B

Nope. If you haven't seen this done before then it will be hard to see on your own, so it's weird you've been assigned this integral.

[math]\frac{4}{1-4t^2}=\frac{A}{1-2t}+\frac{B}{1+2t}[/math]

Now multiply every term by [math]1-4t^2[/math]

[math]4=A(1+2t)+B(1-2t)[/math].

Normally you can't solve a for two variable with only one equation, but there is a nice trick! You can let t be anything you want :) What happens to the above equation if you let [math]t=\frac{1}{2}[/math]?

 

[MarkFL]

I don't think this integral has been assigned. I think the assignment requires the use of the inverse tangent function...(Wink)

 

[MarkFL]

Jameson, I like your approach to the partial fractions, a different take on the Heaviside cover up method I haven't seen before.

 

[karush]

that makes $A=2$ not sure why we can make t anything?

 

[Jameson]

I like your approach to the partial fractions though, a different take on the Heaviside cover up method I haven't seen before.

I deleted my previous post because I thought I was mistaken, but I was doubly-mistaken! Sorry to make it look like you posted twice, haha.

One of the bounds of the integral with $1-4t^2$ won't converge.

Yep, that was the method we learned in class and it works pretty well for most partial fractions. You need to memorize the different cases so you know how to set up the decomposition but once it's set up finding the coefficients is pretty straight-forward.

 

[Jameson]

that makes $A=2$ not sure why we can make t anything?

karush - this definite integral doesn't exist. You've made a typo in your OP or the book made an error.

Wolfram Alpha confirms

 

[karush]

its an AP Calculus practice question,,,, I was going really good thru the problems then boom I hit this one... so its really open game on how you solve it. I just thot log was the way to go...

 

[MarkFL]

...
Yep, that was the method we learned in class and it works pretty well for most partial fractions. You need to memorize the different cases so you know how to set up the decomposition but once it's set up finding the coefficients is pretty straight-forward.

This is the method I was taught in class:

$\displaystyle \frac{4}{1-4t^2}=\frac{A}{1+2t}+\frac{B}{1-2t}$

Multiply through by the denominator on the left:

$\displaystyle 4=A(1-2t)+B(1+2t)$

$\displaystyle 0t+4=(2B-2A)t+(A+B)$

Equating coefficients gives us the system:

$\displaystyle A=B$

$\displaystyle A+B=4$

Hence:

$\displaystyle A=B=2$

Then, one day a kind and knowledgeable chap on MMF introduced me to the Heaviside cover-up method:

Heaviside cover-up method - Wikipedia, the free encyclopedia

 

[soroban]

Hello, karush!

Are you aware of these formulas?

. . $\displaystyle \int \frac{du}{u^2-a^2} \;=\;\frac{1}{2a}\ln\left|\frac{u-a}{u+a}\right|= C$

. . $\displaystyle\int \frac{du}{a^2-u^2} \;=\;\frac{1}{2a}\ln\left|\frac{a+u}{a-u}\right| + C$


It seems that no one teaches them anymore.[rant]

I've posted these formulas at other sites
and have received arguments about them.

The foremost (and most offensive) is:
"I'd rather have my students understand the procedure
rather than memorize a bunch of formulas."

Excuse me . . . but haven't they already memorized a bunch of formulas?
[The Quadratic Formula, the Binomial Theorem, differentiation (power rule,
product rule, quotient rule, chain rule,) integration (power rule, six trig
integrals, six inverse trig integrals, integration by subsitutions, integration
by parts, etc.] .What's two more formulas?

These are same critics who have their students complete-the-square
rather than use the Quadratic Formula.

My response is: suppose you and I go for a job interview.
And they give us $\int\frac{dx}{x^2-9}$ to integrate.

While you are doing Partial Fractions or Trig Substitution,
I have written the answer: .$\frac{1}{6}\ln\left|\frac{x-3}{x+3}\right| + C$
Guess who will get the job?

[/rant]

 

[karush]

no have not seen these, will use tho...

let me get back to this... I am so tired my brain shut off... will reply tomorrow.

And wow, I do learn much here at MHB... I will hang out a lot more and donate.

mahalo...K

View attachment 513

guess many tricks to calculus,,,

 

[CaptainBlack]

Hello, karush!

Are you aware of these formulas?

. . $\displaystyle \int \frac{du}{u^2-a^2} \;=\;\frac{1}{2a}\ln\left|\frac{u-a}{u+a}\right|= C$

. . $\displaystyle\int \frac{du}{a^2-u^2} \;=\;\frac{1}{2a}\ln\left|\frac{a+u}{a-u}\right| + C$


It seems that no one teaches them anymore.[rant]

I've posted these formulas at other sites
and have received arguments about them.

The foremost (and most offensive) is:
"I'd rather have my students understand the procedure
rather than memorize a bunch of formulas."

Excuse me . . . but haven't they already memorized a bunch of formulas?
[The Quadratic Formula, the Binomial Theorem, differentiation (power rule,
product rule, quotient rule, chain rule,) integration (power rule, six trig
integrals, six inverse trig integrals, integration by subsitutions, integration
by parts, etc.] .What's two more formulas?

These are same critics who have their students complete-the-square
rather than use the Quadratic Formula.

My response is: suppose you and I go for a job interview.
And they give us $\int\frac{dx}{x^2-9}$ to integrate.

While you are doing Partial Fractions or Trig Substitution,
I have written the answer: .$\frac{1}{6}\ln\left|\frac{x-3}{x+3}\right| + C$
Guess who will get the job?

[/rant]

Actually at an interview I would ask if I can borrow their copy of Gradshteyn and Ryzhik (or get out a mobile computing device) if they want to see this done in a professional manner.

If they want to see it done by hand I would tell them I don't waste effort on remembering tables, and then work it from more general ideas.

I have had interviews where technical questions were asked and the interviewer was not interested in the answer but the thought processes used to approach the problem.

(And the reason for teaching completing the square is so that the student has some idea where the quadratic formula comes from, and because the technique has other applications which they need one day).

CB

 

[Jameson]

View attachment 513

karush,

That picture shows exactly what MarkFL was suggesting all along - the original problem had a typo in it! You have attached a solution to the integral:

$\displaystyle \int_0^{\frac{1}{2}}\frac{4}{1+4t^2}\,dt$.

You wrote in your original post this integral:

$\displaystyle\int_0^\frac{1}{2}\frac{4}{1-4t^2}dt$

That minus sign instead of a plus sign in the denominator makes a huge difference. Don't worry though, it's easy to make these kinds of oversights :)

Ok, at this point in the thread most of it has been devoted to solving a different integral and there is room for a discussion on how math should be taught to students. Both of these would do better in a new thread though so I will close this thread now purely for organizational reasons.